
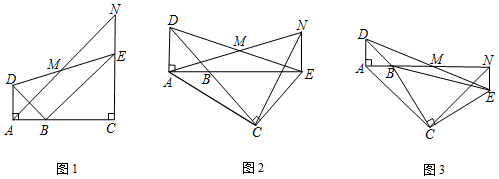
分析 (1)由EN∥AD和点M为DE的中点可以证得△ADM≌△NEM,从而证得M为AN的中点.
(2)易证AB=DA=NE,∠ABC=∠NEC=135°,从而可以证得△ABC≌△NEC,进而可以证得AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
(3)延长AB交NE于点F,易得△ADM≌△NEM,根据四边形BCEF内角和,可得∠ABC=∠FEC,从而可以证得△ABC≌△NEC,进而可以证得AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
解答 (1)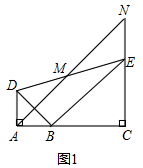 证明:如图1,
证明:如图1,
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,
∴DM=EM.
在△ADM和△NEM中,
$\left\{\begin{array}{l}{∠MAD=∠MNE}\\{∠ADM=∠NEM}\\{DM=EM}\end{array}\right.$.
∴△ADM≌△NEM.
∴AM=MN.
∴M为AN的中点;
(2)证明:如图2,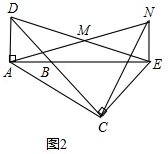
∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,
∴∠DAE+∠NEA=180°.
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=135°.
∵A,B,E三点在同一直线上,
∴∠ABC=180°-∠CBE=135°.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),
∴AD=NE.
∵AD=AB,
∴AB=NE.
在△ABC和△NEC中,
$\left\{\begin{array}{l}{AB=NE}\\{∠ABC=∠NEC}\\{BC=EC}\end{array}\right.$,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形;
(3)△ACN仍为等腰直角三角形.
证明:
∵AD∥NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE.
∵AD∥NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°
∴∠FBC+∠FEC=360°-180°=180°
∵∠FBC+∠ABC=180°
∴∠ABC=∠FEC
在△ABC和△NEC中,
$\left\{\begin{array}{l}{AB=NE}\\{∠ABC=∠NEC}\\{BC=EC}\end{array}\right.$,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
点评 本题考查了全等三角形的判定与性质、平行线的性质、等腰直角三角形的判定与性质、多边形的内角与外角等知识,在(3)中能够在掌握变中有不变的辩证思想是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,∠BAC=90°,AB=6,AC=8.
如图,已知△ABC,∠BAC=90°,AB=6,AC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
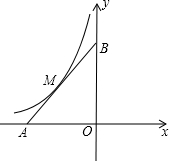 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-$\frac{9}{x}$的图象与线段AB交于M点,且AM=BM.
已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-$\frac{9}{x}$的图象与线段AB交于M点,且AM=BM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
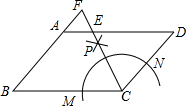 如图,在?ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于4.
如图,在?ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
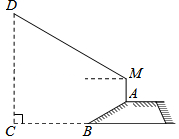 如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.
如图,防洪大堤的横截面是梯形,背水坡AB的坡度i=1:$\sqrt{3}$,AB=20米,身高为1.7米的小明站在大堤A点,测得高压电线杆的顶端D的仰角为30°,已知地而BC宽30米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某学员在广场上练习驾驶汽车,第一次向左拐弯15度行驶一段后,第二次向左拐弯13度,再次行驶一段后,那么第三次要向右拐弯28度,则行驶方向与原来行驶方向相同.
如图,某学员在广场上练习驾驶汽车,第一次向左拐弯15度行驶一段后,第二次向左拐弯13度,再次行驶一段后,那么第三次要向右拐弯28度,则行驶方向与原来行驶方向相同.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com