
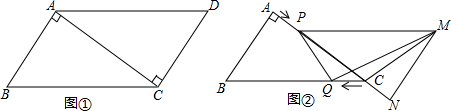
分析 (1)根据勾股定理求出AC,根据PQ∥AB,得出关于t的比例式,求解即可;
(2)过点P作PD⊥BC于D,根据△CPD∽△CBA,列出关于t的比例式,表示出PD的长,再根据S△QMC=$\frac{1}{2}$QC•PD,进行计算即可;
(3)过点M作ME⊥BC的延长线于点E,根据△CPD∽△CBA,得出PD=$\frac{3}{5}$(4-t),CD=$\frac{4}{5}$(4-t),再根据△PDQ∽△QEM,得到 $\frac{PD}{QE}$=$\frac{DQ}{EM}$,即PD•EM=QE•DQ,进而得到方程($\frac{12}{5}$-$\frac{3}{5}$t)2=($\frac{16}{5}$-$\frac{9}{5}$t)($\frac{9}{5}$+$\frac{9}{5}$t),求得t=$\frac{3}{2}$或t=0(舍去),即可得出当t=$\frac{3}{2}$时,PQ⊥MQ.
解答 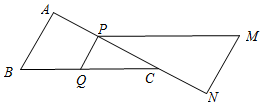 解:(1)如图所示,AB=3cm,BC=5cm,AC⊥AB,
解:(1)如图所示,AB=3cm,BC=5cm,AC⊥AB,
∴Rt△ABC中,AC=4,
若PQ∥AB,则有$\frac{CP}{PA}$=$\frac{CQ}{QB}$,
∵CQ=PA=t,CP=4-t,QB=5-t,
∴$\frac{4-t}{t}$=$\frac{t}{5-t}$,
即20-9t+t2=t2,
解得t=$\frac{20}{9}$,
当t=$\frac{20}{9}$时,PQ∥AB;
(2)如图所示,过点P作PD⊥BC于点D,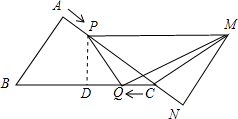
∴∠PDC=∠A=90°,
∵∠PCD=∠BCA
∴△CPD∽△CBA,
∴$\frac{CP}{CB}$=$\frac{PD}{BA}$,
当t=3时,CP=4-3=1,
∵BA=3,BC=5,
∴$\frac{1}{5}$=$\frac{PD}{3}$,
∴PD=$\frac{3}{5}$,
又∵CQ=3,PM∥BC,
∴S△QMC=$\frac{1}{2}$×3×$\frac{3}{5}$=$\frac{9}{10}$;
(3)存在时刻t=$\frac{3}{2}$,使PQ⊥MQ,
理由如下:如图所示,过点M作ME⊥BC的延长线于点E,
∵△CPD∽△CBA,
∴$\frac{CP}{CB}$=$\frac{PD}{BA}$=$\frac{CD}{CA}$,
∵BA=3,CP=4-t,BC=5,CA=4,
∴$\frac{4-t}{5}$=$\frac{PD}{3}$=$\frac{CD}{4}$,
∴PD=$\frac{3}{5}$(4-t),CD=$\frac{4}{5}$(4-t).
∵PQ⊥MQ,
∴∠PDQ=∠QEM=90°,∠PQD=∠QME,
∴△PDQ∽△QEM,
∴$\frac{PD}{QE}$=$\frac{DQ}{EM}$,即PD•EM=QE•DQ.
∵EM=PD=$\frac{3}{5}$(4-t)=$\frac{12}{5}$-$\frac{3}{5}$t,
DQ=CD-CQ=$\frac{4}{5}$(4-t)-t=$\frac{16}{5}$-$\frac{9}{5}$t,
QE=DE-DQ=5-[$\frac{4}{5}$(4-t)-t]=$\frac{9}{5}$+$\frac{9}{5}$t,
∴($\frac{12}{5}$-$\frac{3}{5}$t)2=($\frac{16}{5}$-$\frac{9}{5}$t)($\frac{9}{5}$+$\frac{9}{5}$t),
即2t2-3t=0,
∴t=$\frac{3}{2}$或t=0(舍去),
∴当t=$\frac{3}{2}$时,PQ⊥MQ.
点评 此题属于四边形综合题,主要考查了相似三角形的判定与性质、勾股定理、平行线的性质、三角形的面积计算的综合应用,解决问题的关键是根据题意画出图形,作出辅助线,构造相似三角形.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
估算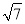 的值是( )
的值是( )
A. 在1和2之间 B. 在2和3之间
C. 在3和4之间 D. 在4和5之间
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
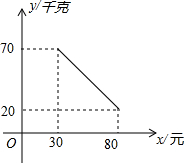 某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.
某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
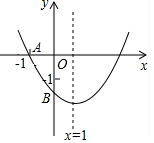 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
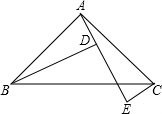 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.
如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com