
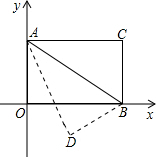
 已知:如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A坐标为(0,6),∠OAB=60°,以AB为轴对折后,使C点落在D点处,则D点坐标(3$\sqrt{3}$,-3).
已知:如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A坐标为(0,6),∠OAB=60°,以AB为轴对折后,使C点落在D点处,则D点坐标(3$\sqrt{3}$,-3). 分析 根据点A的坐标求出OA,再根据直角三角形30°角所对的直角边等于斜边的一半求出求出AB,然后利用勾股定理列式求出OB,然后根据矩形的性质可得AC=OB,再求出∠CAB=30°,根据翻折变换的性质可得∠BAD=∠CAB,AD=AC,然后求出∠DAO=30°,过点D作DE⊥y轴于E,根据直角三角形30°角所对的直角边等于斜边的一半求出DE,利用勾股定理列式求出AE,再求出OE,最后写出点D的坐标即可.
解答  解:∵点A坐标为(0,6),
解:∵点A坐标为(0,6),
∴OA=6,
∵∠OAB=60°,
∴∠ABO=90°-60°=30°,
∴AB=2OA=2×6=12,
由勾股定理得,OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∴AC=OB=6$\sqrt{3}$,
∵∠OAB=60°,
∴∠BAC=90°-60°=30°,
由翻折变换的性质得,∠BAD=∠CAB=30°,AD=AC=6$\sqrt{3}$,
∴∠DAO=∠OAB-∠BAD=60°-30°=30°,
过点D作DE⊥y轴于E,则DE=$\frac{1}{2}$AD=$\frac{1}{2}$×6$\sqrt{3}$=3$\sqrt{3}$,
由勾股定理得,AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{(6\sqrt{3})^{2}-(3\sqrt{3})^{2}}$=9,
所以,OE=AE-OA=9-6=3,
∵点D在第四象限,
∴点D的坐标为(3$\sqrt{3}$,-3).
故答案为:(3$\sqrt{3}$,-3).
点评 本题考查了翻折变换的性质,矩形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质以及勾股定理,翻折前后对应边相等,对应角相等.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
 某单位准备将院内一块长30m,宽20m的长方形空土,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?
某单位准备将院内一块长30m,宽20m的长方形空土,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com