练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，三个等圆两两外切于点A﹑B﹑C，在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P，边接PA﹑PB﹑PC，试问:以PA﹑PB﹑PC为边长能否组成一个锐角三角形? 证明你的结论。
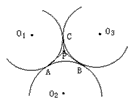
    解：以PA、PB、PC为边长能组成一个锐角三角形，
      证明如下： 连接O1O2、O1O3、O2O3，AB、BC、AC，
      易证△O1O2O3，△ABC都是正三角形
       把△APB绕点A旋转60°至△ACPˊ，得△APPˊ是正三角形 PˊC=PB ，PA=P Pˊ
       ∴△PPˊC就是以PA、PB、PC的边长组成的三角形
      记∠APB=α，∠BPC=β，∠APC=γ
       ∵P在正三角形ABC的内部
       ∴α＞60°，β＞60°，γ＞60°
      又∵P在弧AB的外部，弧AB所含的圆周角为150°
       ∴α＜150°，同理β＜150°，γ＜150° 
       ∵∠PPˊC=∠A PˊC-60°=α-60°，
      ∠C PPˊ=∠CPA-60°=γ-60°
        ∴∠PˊCP=180°-（α-60°）-（γ-60°）=300°-（α+γ）=β-60°，
        ∵60°＜α，β，γ＜150°
        ∴0°＜α-60°，β-60°，γ-60°＜90°
        ∴△PPˊC为锐角三角形
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

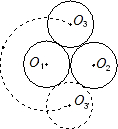    精英家教网如图，三个半径为1的等圆两两相外切，则中间围成的阴影部分面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，三个半径为1的等圆两两外切，若固定⊙O1和⊙O2，将⊙O3沿⊙O1的边缘逆时针旋转到⊙O3′的位置（即⊙O1、⊙O2、⊙O3′两两外切），圆心O3所经过的路程为（　　）
    A、2π
    B、
    4
    3
    π
    C、
    8
    3
    π
    D、4π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

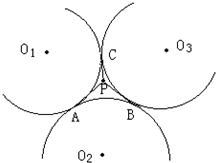    如图，三个等圆两两外切于点A﹑B﹑C，在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P，边接PA﹑PB﹑PC，试问：以PA﹑PB﹑PC为边长能否组成一个锐角三角形？证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，三个等圆两两外切于点A﹑B﹑C，在圆弧AB﹑BC﹑CA所围成的曲线区域内任取一点P，边接PA﹑PB﹑PC，试问：以PA﹑PB﹑PC为边长能否组成一个锐角三角形？证明你的结论．

    查看答案和解析>>

    同步练习册答案