
【题目】已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
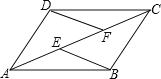
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
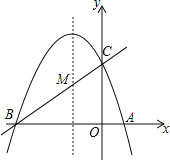
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=-1是关于x的方程a+bx=-2的解,则代数式2015-a+b的值为( )
A. 2013 B. 2015 C. 2017 D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=5x2向右平移2个单位,再向上平移3个单位,得到的新抛物线的顶点坐标是( )
A.(2,3)
B.(﹣2,3)
C.(2,﹣3)
D.(﹣2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数图象如图,请结合图象信息解答下列问题:
(小时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)求慢车的行驶速度和![]() 的值;
的值;
(2)求快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)求两车出发后几小时相距的路程为![]() 千米?
千米?
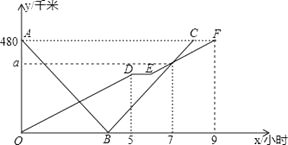
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 3. 6 | 3.6 | 7.4 | 8.1 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择【 】
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按图填空, 并注明理由
已知: 如图, ∠1=∠2, ∠3=∠E. 求证: AD∥BE
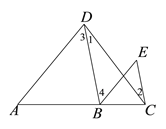
证明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代换 )
∴ ∥ ( 内错角相等,两直线平行 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com