
 某校期中考试后,为了更好地了解七年级测试的数学成绩情况,随机抽取了部分学生的试卷.对学生的数学成绩(得分取整数)进行赘理.分成五组,并绘制成如下不完整的频数分布直方图.在直方图中从左到右依次为一、二、三、四、五组.成绩没有低于20分的,第五组的人数占抽样人数的30%.第四组的人数是第二组的人数的4倍.请结合信息回答下列问题.
某校期中考试后,为了更好地了解七年级测试的数学成绩情况,随机抽取了部分学生的试卷.对学生的数学成绩(得分取整数)进行赘理.分成五组,并绘制成如下不完整的频数分布直方图.在直方图中从左到右依次为一、二、三、四、五组.成绩没有低于20分的,第五组的人数占抽样人数的30%.第四组的人数是第二组的人数的4倍.请结合信息回答下列问题.分析 (1)根据统计图可以求得样本容量;
(2)根据题意可以求得第二组和第四组的人数,从而可以将频数分布直方图补充完整;
(3)根据题意可以求得各组所占的百分比,从而可以将扇形统计图补充完整,求得第四组所在扇形图的圆心角度数;
(4)根据统计图中的数据可以求得我校七年级900名学生成绩在20.5一40.5范围的学生人数.
解答 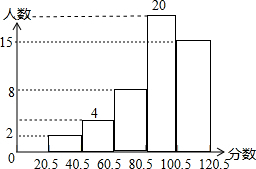 解:(1)抽取的样本容量是:15÷30%=50,
解:(1)抽取的样本容量是:15÷30%=50,
即抽取的样本容量是50;
(2)设第二组有x人,则第四组的人数为4x人,
x+4x=50-2-8-15,
解得,x=5,
则4x=20
即第二组有5人,第四组有20人,
故频数分布直方图如右图所示,
(3)第一组占得百分比为:2÷50×100%=4%,
第二组占得百分比为:5÷50×100%=10%,
第三组占得百分比为:8÷50×100%=16%,
第四组占得百分比为:20÷50×100%=40%,
第五组占得百分比为:30%,
绘制的扇形统计图如右图所示,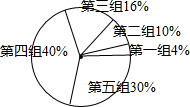
第四组所在扇形图的圆心角度数是:40%×360°=144°;
(4)900×$\frac{2}{50}$=36(人),
即成绩在20.5一40.5范围的学生大约有36人.
点评 本题考查频数分布直方图、扇形统计图、总体、个体、样本、样本容量,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点D、E分别在△ABC的边AB、AC上,如果$\frac{DE}{BC}$=$\frac{AD}{AB}$,那么能否得到DE∥BC,为什么?
如图,点D、E分别在△ABC的边AB、AC上,如果$\frac{DE}{BC}$=$\frac{AD}{AB}$,那么能否得到DE∥BC,为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com