
”¾ĢāÄæ”æĪŅĆĒ¶ØŅå£ŗĮ½±ßĘ½·½ŗĶµČÓŚµŚČż±ßĘ½·½µÄ2±¶µÄČż½ĒŠĪ½Š×öĘęŅģČż½ĒŠĪ£®
ĄżČē£ŗÄ³Čż½ĒŠĪČż±ß³¤·Ö±šŹĒ2£¬4£¬![]() £¬ŅņĪŖ
£¬ŅņĪŖ![]() £¬ĖłŅŌÕāøöČż½ĒŠĪŹĒĘęŅģČż½ĒŠĪ£®
£¬ĖłŅŌÕāøöČż½ĒŠĪŹĒĘęŅģČż½ĒŠĪ£®
£Ø1£©øł¾Ż¶ØŅå£ŗ”°µČ±ßČż½ĒŠĪŹĒĘęŅģČż½ĒŠĪ”±ÕāøöĆüĢāŹĒ______ĆüĢā£ØĢī”°Õę”±»ņ”°¼ŁĆüĢā”±£©£»
£Ø2£©ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬Čō
£¬Čō![]() ŹĒĘęŅģČż½ĒŠĪ£¬Ēó
ŹĒĘęŅģČż½ĒŠĪ£¬Ēó![]() £»
£»
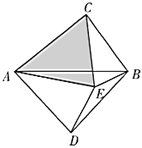
£Ø3£©ČēĶ¼£¬ŅŌ![]() ĪŖŠ±±ß·Ö±šŌŚ
ĪŖŠ±±ß·Ö±šŌŚ![]() µÄĮ½²ą×÷Ö±½ĒČż½ĒŠĪ£¬ĒŅ
µÄĮ½²ą×÷Ö±½ĒČż½ĒŠĪ£¬ĒŅ![]() £¬ČōĖıߊĪ
£¬ČōĖıߊĪ![]() ÄŚ“ęŌŚµć
ÄŚ“ęŌŚµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() £¬
£¬![]() £®
£®
¢ŁĒóÖ¤£ŗ![]() ŹĒĘęŅģČż½ĒŠĪ£»
ŹĒĘęŅģČż½ĒŠĪ£»
¢Śµ±![]() ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬Ēó
ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬Ēó![]() µÄ¶ČŹż£®
µÄ¶ČŹż£®
”¾“š°ø”æ£Ø1£©Õę£»£Ø2£©![]() £»£Ø3£©¢ŁÖ¤Ć÷¼ū½āĪö£»¢Ś
£»£Ø3£©¢ŁÖ¤Ć÷¼ū½āĪö£»¢Ś![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©ÉčµČ±ßČż½ĒŠĪµÄ±ß³¤ĪŖa£¬Ōņa2+a2=2a2£¬¼“æÉµĆ³ö½įĀŪ£»
£Ø2£©Óɹ“¹É¶ØĄķµĆ³öa2+b2=c2¢Ł£¬ÓÉRt”÷ABCŹĒĘęŅģČż½ĒŠĪ£¬ĒŅb£¾a£¬µĆ³öa2+c2=2b2¢Ś£¬ÓÉ¢Ł¢ŚµĆ³öb=![]() a£¬c=
a£¬c=![]() a£¬¼“æÉµĆ³ö½įĀŪ£»
a£¬¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©¢ŁÓɹ“¹É¶ØĄķµĆ³öAC2+BC2=AB2£¬AD2+BD2=AB2£¬ÓÉŅŃÖŖµĆ³ö2AD2=AB2£¬AC2+CE2=2AE2£¬¼“æÉµĆ³ö”÷ACEŹĒĘęŅģČż½ĒŠĪ£»
¢ŚÓÉ”÷ACEŹĒĘęŅģČż½ĒŠĪ£¬µĆ³öAC2+CE2=2AE2£¬·ÖĮ½ÖÖĒéæö£¬ÓÉÖ±½ĒČż½ĒŠĪŗĶĘęŅģČż½ĒŠĪµÄŠŌÖŹ¼“æÉµĆ³ö“š°ø£®
£Ø1£©½ā£ŗ”°µČ±ßČż½ĒŠĪŹĒĘęŅģČż½ĒŠĪ”±ÕāøöĆüĢāŹĒÕęĆüĢā£¬ĄķÓÉČēĻĀ£ŗ
ÉčµČ±ßČż½ĒŠĪµÄŅ»±ßĪŖ![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
”ą·ūŗĻĘęŅģČż½ĒŠĪ”±µÄ¶ØŅ壮
£Ø2£©½ā£ŗ”ß![]() £¬Ōņ
£¬Ōņ![]() ¢Ł£¬
¢Ł£¬
”ß![]() ŹĒĘęŅģČż½ĒŠĪ£¬ĒŅ
ŹĒĘęŅģČż½ĒŠĪ£¬ĒŅ![]() £¬
£¬
”ą![]() ¢Ś£¬
¢Ś£¬
ÓÉ¢Ł¢ŚµĆ£ŗ![]() £¬
£¬![]() £¬
£¬
”ą![]() £®
£®
£Ø3£©¢ŁÖ¤Ć÷£ŗ”ß![]() £¬
£¬
”ą![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() ŹĒĘęŅģČż½ĒŠĪ£®
ŹĒĘęŅģČż½ĒŠĪ£®
¢ŚÓÉ¢ŁæɵĆ![]() ŹĒĘęŅģČż½ĒŠĪ£¬
ŹĒĘęŅģČż½ĒŠĪ£¬
”ą![]() £¬
£¬
µ±![]() ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬
ŹĒÖ±½ĒČż½ĒŠĪŹ±£¬
ÓÉ£Ø2£©µĆ£ŗ![]() »ņ
»ņ![]() £¬
£¬
µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬
¼“![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £®
£®
µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬
¼“![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() ”ć£¬
”ć£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() »ņ
»ņ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
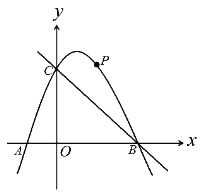
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¶ž“ĪŗÆŹż![]() µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£¬ ÓėyÖį½»ÓŚC£Ø0,3£©£¬AµćŌŚŌµćµÄ×ó²ą£¬BµćµÄ×ų±źĪŖ£Ø3,0£©£©”£µćPŹĒÅ×ĪļĻßÉĻŅ»øö¶Æµć£¬ĒŅŌŚÖ±ĻßBCµÄÉĻ·½.
µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£¬ ÓėyÖį½»ÓŚC£Ø0,3£©£¬AµćŌŚŌµćµÄ×ó²ą£¬BµćµÄ×ų±źĪŖ£Ø3,0£©£©”£µćPŹĒÅ×ĪļĻßÉĻŅ»øö¶Æµć£¬ĒŅŌŚÖ±ĻßBCµÄÉĻ·½.
£Ø1£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½.
£Ø2£©Į¬½ÓPO”¢PC£¬²¢°Ń”÷POCŃŲCO·ÕŪ£¬µĆµ½ĖıߊĪ![]() £¬ÄĒĆ“ŹĒ·ń“ęŌŚµćP£¬Ź¹ĖıߊĪ
£¬ÄĒĆ“ŹĒ·ń“ęŌŚµćP£¬Ź¹ĖıߊĪ![]() ĪŖĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±µćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
ĪŖĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±µćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
£Ø3£©µ±µćPŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬Ź¹”÷BPCµÄĆ껿×ī“ó£¬Ēó³öµćPµÄ×ų±źŗĶ”÷BPCµÄĆ껿×ī“óÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼µćA£Ø1£¬1£©£¬B£Ø2£¬©3£©£¬µćPĪŖxÖįÉĻŅ»µć£¬µ±|PA©PB|×ī“óŹ±£¬µćPµÄ×ų±źĪŖ£Ø””””£©

A. £Ø©1£¬0£© B. £Ø![]() £¬0£© C. £Ø
£¬0£© C. £Ø![]() £¬0£© D. £Ø1£¬0£©
£¬0£© D. £Ø1£¬0£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹży=kx+bÓė·“±ČĄżŗÆŹży=![]() £Øm”Ł0£©µÄĶ¼Ļó½»ÓŚµćA£Ø3£¬1£©£¬ĒŅ¹żµćB£Ø0£¬©2£©£®
£Øm”Ł0£©µÄĶ¼Ļó½»ÓŚµćA£Ø3£¬1£©£¬ĒŅ¹żµćB£Ø0£¬©2£©£®
£Ø1£©Ē󷓱ȥżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©Čē¹ūµćPŹĒxÖįÉĻŅ»µć£¬ĒŅ”÷ABPµÄĆ껿ŹĒ3£¬ĒóµćPµÄ×ų±ź£®
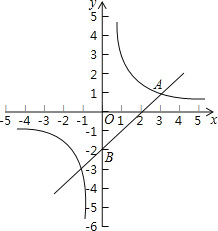
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
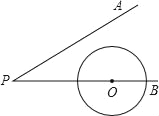
”¾ĢāÄæ”æČēĶ¼£¬”ĻAPB=30”ć£¬Ō²ŠÄŌŚPBÉĻµÄ”ŃOµÄ°ė¾¶ĪŖ1cm£¬OP=3cm£¬Čō”ŃOŃŲBP·½ĻņĘ½ŅĘ£¬µ±”ŃOÓėPAĻąĒŠŹ±£¬Ō²ŠÄOĘ½ŅĘµÄ¾ąĄėĪŖ_____cm£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
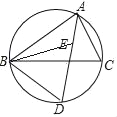
”¾ĢāÄæ”æČēĶ¼£¬µćEŹĒ”÷ABCµÄÄŚŠÄ£¬AEµÄŃÓ³¤ĻßÓė”÷ABCµÄĶā½ÓŌ²Ļą½»ÓŚµćD£®
(1)Čō”ĻBAC=70”ć£¬Ēó”ĻCBDµÄ¶ČŹż£»
(2)ĒóÖ¤£ŗDE=DB£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°Ą¬»ų²»ĀäµŲ£¬³ĒŹŠøüĆĄĄö”±£®Ä³ÖŠŃ§ĪŖĮĖĮĖ½āĘßÄź¼¶Ń§Éś¶ŌÕāŅ»³«ŅéµÄĀ䏵Ēéæö£¬Ń§Š£°²ÅÅÕž½Ģ“¦ŌŚĘßÄź¼¶Ń§ÉśÖŠĖ껜³éČ”ĮĖ²æ·Öѧɜ£¬²¢Õė¶Ōѧɜ”°ŹĒ·ńĖęŹÖ¶ŖĄ¬»ų”±ÕāŅ»Ēéæö½ųŠŠĮĖĪŹ¾ķµ÷²é£¬Ķ³¼Ę½į¹ūĪŖ£ŗAĪŖ“Ó²»ĖęŹÖ¶ŖĄ¬»ų£»BĪŖż¶ūĖęŹÖ¶ŖĄ¬»ų£»CĪŖ¾³£ĖęŹÖ¶ŖĄ¬»ųČżĻī£®ŅŖĒóĆæĪ»±»µ÷²éµÄѧɜ±ŲŠė“ÓŅŌÉĻČżĻīÖŠŃ”Ņ»ĻīĒŅÖ»ÄÜŃ”Ņ»Ļī£®ĻÖ½«µ÷²é½į¹ū»ęÖĘ³ÉŅŌĻĀĄ“²»¹¼øŗ²»ĶźÕūµÄĶ³¼ĘĶ¼£®
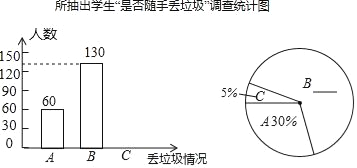
ĒėÄćøł¾ŻŅŌÉĻŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
(1)²¹Č«ÉĻĆęµÄĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£»
(2)Ėł³éȔѧɜ”°ŹĒ·ńĖęŹÖ¶ŖĄ¬»ų”±ĒéæöµÄÖŚŹżŹĒ”” ””£»
(3)ČōøĆŠ£ĘßÄź¼¶¹²ÓŠ1500Ćūѧɜ£¬ĒėÄć¹Ą¼ĘøĆÄź¼¶Ń§ÉśÖŠ”°¾³£ĖęŹÖ¶ŖĄ¬»ų”±µÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æĢøĢøÄćµÄæ“·Ø£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB£½90”ć£¬DŹĒBCµÄÖŠµć£¬DE”ĶBC£¬CE//AD£¬ČōAC£½2£¬CE£½4£¬ŌņĖıߊĪACEBµÄÖܳ¤ĪŖ ”ų £®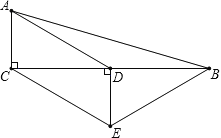
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŹżŃ§æĪÉĻ£¬ĄĻŹ¦Ģį³öŅ»øöĪŹĢā”°ÓĆÖ±³ßŗĶŌ²¹ę×÷Ņ»øö¾ŲŠĪ”±£®
Š”»ŖµÄ×ö·ØČēĻĀ£ŗ
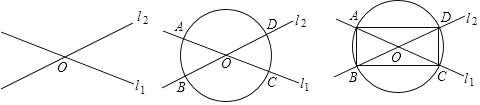
![]() ČēĶ¼1£¬ČĪČ”Ņ»µćO£¬¹żµćO×÷Ö±Ļßl1£¬l2£»
ČēĶ¼1£¬ČĪČ”Ņ»µćO£¬¹żµćO×÷Ö±Ļßl1£¬l2£»![]() ČēĶ¼2£¬ŅŌOĪŖŌ²ŠÄ£¬ČĪŅā³¤ĪŖ°ė¾¶×÷Ō²£¬ÓėÖ±Ļßl1£¬l2·Ö±šĻą½»ÓŚµćA”¢C£¬B”¢D£»
ČēĶ¼2£¬ŅŌOĪŖŌ²ŠÄ£¬ČĪŅā³¤ĪŖ°ė¾¶×÷Ō²£¬ÓėÖ±Ļßl1£¬l2·Ö±šĻą½»ÓŚµćA”¢C£¬B”¢D£»![]() ČēĶ¼3£¬Į¬½ÓAB”¢BC”¢CD”¢DAĖıߊĪABCD¼“ĪŖĖłĒó×÷µÄ¾ŲŠĪ£®
ČēĶ¼3£¬Į¬½ÓAB”¢BC”¢CD”¢DAĖıߊĪABCD¼“ĪŖĖłĒó×÷µÄ¾ŲŠĪ£®
ĄĻŹ¦Ėµ£ŗ”°Š”»ŖµÄ×÷·ØÕżČ·”±£®
Ēė»Ų“š£ŗŠ”»ŖµÄ×÷Ķ¼ŅĄ¾ŻŹĒ______£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com