
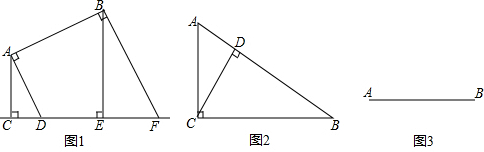
分析 (1)根据两图形之间距离定义,得出线段AB和直线l的距离即可;
(2)首先过点D作DE⊥BC于点E,进而利用直角三角形中30°所对的边等于斜边的一半,进而求出DE的长;
(3)根据两图形之间距离定义,利用CD的长为1cm,且线段CD与已知线段AB的距离为1.5cm,得出符合题意的图形是两个半圆以及矩形组成的图形.
解答  解:(1)如图所示:过A,B分别作垂线段AC、AD、BE、BF,
解:(1)如图所示:过A,B分别作垂线段AC、AD、BE、BF,
则线段AB和直线l的距离为垂线段为:AC的长度;
故答案为:AC;
(2)如图2,过点D作DE⊥BC于点E,
∵∠ACB=90°,∠B=30°,CD⊥AB,AD=2,
∴∠A=60°则∠ACD=30°,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=6,
则DE=$\frac{1}{2}$BD=3;
故答案为:3;
(3)如图3所示: .
.
点评 此题主要考查了应用设计与作图以及新定义,根据题意争正确把握两图形之间距离定义是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | … |
| A. | $\frac{8}{61}$ | B. | $\frac{8}{63}$ | C. | $\frac{8}{65}$ | D. | $\frac{8}{67}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
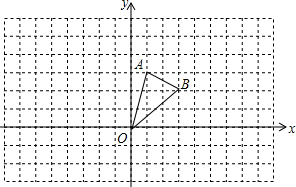 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.
如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4)、B(-3,1)、C(-3,4),△A1B1C1是由△ABC绕某一点顺时针旋转得到的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 手机品牌 | 芒果手机 | 四星手机 | 大米手机 |
| 销售量(台) | 200 | 80 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
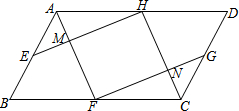 如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com