
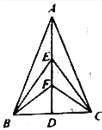
【题目】如图,在△ABC中,AB=AC,点EF是中线AD上的两点,则图中全等三角形有几对( )
A.4对B.5对C.6对D.7对
【答案】C
【解析】
根据三角形全等的判定定理判断每一对三角形即可得出答案.
∵AB=AC,AD是△ABC的中线
∴∠BAD=∠CAD,∠ADB=∠ADC=90°
在△ABD和△ACD中

∴△ABD≌△ACD(SAS)
在△ABE和△ACE中
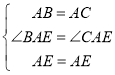
∴△ABE≌△ACE(SAS)
∴∠AEB=∠AEC
∴∠BEF=∠CEF
在△ABF和△ACF中

∴△ABF≌△ACF(SAS)
∴∠AFB=∠AFC
∴∠BFD=∠CFD
在△BEF和△CEF中
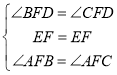
∴△BEF≌△CEF(ASA)
在△BFD和△CFD中
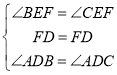
∴△BFD≌△CFD(ASA)
在△BED和△CED中

∴△BED≌△CED(ASA)
共有6对全等三角形,故答案选择C.


科目:初中数学 来源: 题型:
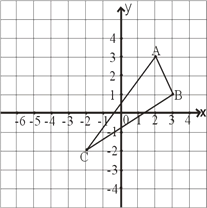
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标.D、E、F点的坐标是:D( , ) E( , ) F( , );
(2)求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,E在线段AC上,连接AD, BE的延长线交AD于F.
(1)猜想线段BE、AD的数量关系和位置关系:_______________(不必证明);
(2)当点E为△ABC内部一点时,使点D和点E分别在AC的两侧,其它条件不变.
①请你在图2中补全图形;
②(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com