
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
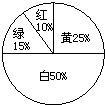 21、某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
21、某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.查看答案和解析>>
科目:初中数学 来源: 题型:
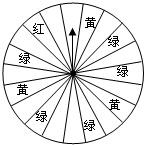 某商场为了吸引顾客,设立了一个可以自由转动的转盘.并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得100元、50元、20元购物券(转盘被等分成20个扇形),甲顾客购物120元,他获得购物卷的概率是多少?
某商场为了吸引顾客,设立了一个可以自由转动的转盘.并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得100元、50元、20元购物券(转盘被等分成20个扇形),甲顾客购物120元,他获得购物卷的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
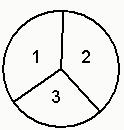 指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.
指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.查看答案和解析>>
科目:初中数学 来源: 题型:
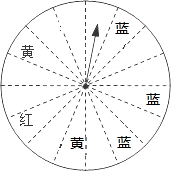 某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为
某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com