
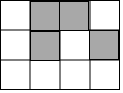
 如图,在4×3长方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×3长方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
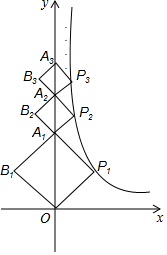 如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、…、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、…、An-1An都在y轴上(n≥1的整数),点P1(x1,y1),点P2(x2,y2),…,Pn(xn,yn)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,并已知B1(-1,1).
如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、…、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、…、An-1An都在y轴上(n≥1的整数),点P1(x1,y1),点P2(x2,y2),…,Pn(xn,yn)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,并已知B1(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
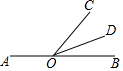 如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为( )
如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为( )| A. | 30° | B. | 31° | C. | 30°30′ | D. | 31°30′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/盏) | 售价(元/盏) | |
| A | 30 | 45 |
| B | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com