
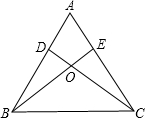
 已知:如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,
已知:如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,分析 (1)只要证明△BDC≌△CEB(AAS),推出∠DBC=∠ECB,即可证明AB=AC;
(2)连接OA,只要证明△ADO≌△AEO(HL),推出∠DAO=∠EAO即可解决问题;
解答 (1)证明:∵OB=OC,
∴∠OBC=∠OCB
∵BE、CD是两条高,
∴∠BDC=∠CEB=90°.
又∵BC=CB,
∴△BDC≌△CEB(AAS),
∴∠DBC=∠ECB,
∴AB=AC,
∴△ABC是等腰三角形.
(2)点O在∠BAC的角平分线上.连接AO.
∵△BDC≌△CEB,
∴DC=EB,
∵OB=OC,
∴OD=OE,
又∵∠ADC=∠AEB=90°,AO=AO,
∴△ADO≌△AEO(HL),
∴∠DAO=∠EAO,
∴点O在∠BAC的角平分线上.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质和判定等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
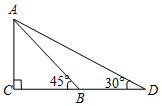 如图,为安全起见,幼儿园打算加长滑梯AB,将其倾斜角由45°降至30°,已知滑梯AB的长为4m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
如图,为安全起见,幼儿园打算加长滑梯AB,将其倾斜角由45°降至30°,已知滑梯AB的长为4m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,∠B=∠C=40°,点E、F在BC边上,∠AEF=70°,∠AFE=60°,求线段BE、EF、CF围成的三角形的各内角度数.
如图,△ABC中,AB=AC,∠B=∠C=40°,点E、F在BC边上,∠AEF=70°,∠AFE=60°,求线段BE、EF、CF围成的三角形的各内角度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com