
【题目】某种植户计划将一片荒山改良后种植沃柑,经市场调查得知,当种植沃柑的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系:y=kx+b,并且当x=20时,y=1800;当x=25时,y=1700.
(1)请求出y与x的函数关系式,并写出自变量的取值范围;
(2)设种植户种植x亩沃柑所获得的总利润为w元,由于受条件限制,种植沃柑面积x不超过50亩,求该种植户种植多少亩获得的总利润最大,并求总利润w(元)的最大值.
【答案】(1)y=﹣20x+2200(15<x≤110);(2)当种植50亩时获利最大,总利润的最大值为60000元
【解析】
(1)根据题意设y=kx+b,再运用待定系数法求解可得;
(2)根据总利润=每亩利润×亩数,分0<x≤15和15<x≤110两种情况分别求解可得.
解:(1)y=kx+b,
将x=20、y=1800和x=25、y=1700代入得:
![]()
解得:![]()
∴y=﹣20x+2200
∵-20x+2200≥0,
解得:x≤110,
∴自变量的取值范围是:15<x≤110;
(2)当0<x≤15时,W=1900x,
∴当x=15时,W最大=28500(元);
当15<x≤110时,
W=(﹣20x+2200)x=﹣20x2+2200x=﹣20(x﹣55)2+60500
∵x≤50
∴当x=50时,W最大=60000(元);
所以,当种植50亩时获利最大,总利润的最大值为60000元.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),与y轴的交点为C,已知﹣2≤c≤﹣1,顶点坐标为(1,n),则下列结论正确的是( )

A.a+b>0
B.![]()
C.对于任意实数m,不等式a+b>am2+bm恒成立
D.关于x的方程ax2+bx+c=n+1没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校鼓励师生利用课余时间广泛阅读,为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下单位:min)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
分段整理样本数据:
课外阅读时间 |
|
|
|
|
等级 | D | C | B | A |
人数 | 3 | ① | 8 | ② |
统计量:
平均数 | 中位数 | 众数 |
80 | ③ | ④ |
得出结论:
(1)填写表格中的数据:
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
|
|
| |
笔试 |
|
|
|
口试 |
|
|
|
形象 |
|
|
|
平均分 |
|
|
|
(1)①![]() ;
;
②在表格中的![]() 个数的中位数是 ,众数是
个数的中位数是 ,众数是
(2)经学校研究决定,在![]() 两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分
两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分![]() 进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?
进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,口罩供不应求.某口罩企业为指导生产,在二月份期间对甲乙丙丁四条生产线日产量进行调研,根据调研数据,绘制出如下两幅不完整的统计图.观察统计图,请解答以下问题:
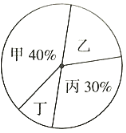

(1)求二月份该企业口罩单日产量(二月份计![]() 天).
天).
(2)求乙条生产线单日产量是多少,并补全频数分布直方图.
(3)为满足市场需求,该公司改进生产技术,使得口罩产量在二月的基础上逐月提高,已知![]() 月份口罩产量为
月份口罩产量为![]() 万只,若三月份和四月份口罩月产量平均增长率相同,求每月的平均增长率.
万只,若三月份和四月份口罩月产量平均增长率相同,求每月的平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上一点,且∠BGC=90°,延长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的长为( )
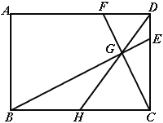
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.
(1)当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是_____ cm.
(2)当夹子的开口最大(点C与点D重合)时,A,B两点的距离为_____cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com