
 如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )
如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )| A. | $y=\frac{{\sqrt{3}}}{5}x+5$ | B. | $y=\sqrt{3}x+5$ | C. | $y=\sqrt{3}x-5$ | D. | $y=-\frac{{\sqrt{3}}}{3}x+5$ |
分析 根据等腰直角三角形的性质和三角函数分别求B、C两点的坐标,利用待定系数法求直线的表达式.
解答  解:∵A点坐标为(5,0),
解:∵A点坐标为(5,0),
∴OA=5,
∵∠BCA=60°,∠α=105°,
∴∠BAC=105°-60°=45°,
∴△AOB是等腰直角三角形,
∴AO=BO=5,
∴B(0,5).
∵∠CBO=90°-∠BCA=30°,
∴BC=2CO,BO=$\sqrt{B{C}^{2}-C{O}^{2}}$=$\sqrt{3}$CO=5,
∴CO=$\frac{5\sqrt{3}}{3}$,
∴C(-$\frac{5\sqrt{3}}{3}$,0),
把B(0,5)和C(-$\frac{5\sqrt{3}}{3}$,0)代入y=kx+b中得:
$\left\{\begin{array}{l}{b=5}\\{-\frac{5\sqrt{3}}{3}k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=5}\end{array}\right.$,
∴直线BC的表达式为:y=$\sqrt{3}$x+5.
故选B.
点评 本题考查了利用待定系数法求直线的解析式、含30度角的直角三角形、等腰直角三角形的性质及图形与坐标特点,熟练掌握图形与坐标特点是本题的关键.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
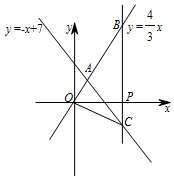 如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.
如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
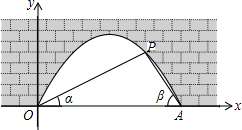 图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tanβ=$\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.
图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=$\frac{1}{2}$,tanβ=$\frac{3}{2}$,以O为原点,OA所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{11}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
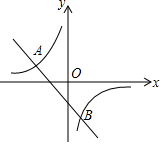 如图,已知A(n,2)、B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(n,2)、B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com