
ЁОЬтФПЁПвбжЊКЏЪ§ЕФЙиЯЕЪНЪЧL1ЃКy=kx2+ЃЈkЉ2ЃЉxЉ2
ЃЈ1ЃЉЯТСаЫЕЗЈжае§ШЗЕФађКХга ЃК
ЂйЕБk=1ЪБЃЌЦфЖЅЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБk=2ЪБЃЌЖўДЮКЏЪ§ЕФЭМЯѓЙигкyжсЖдГЦЃЛ
ЂлЮоТлkЮЊКЮЗЧСужЕЃЌЖўДЮКЏЪ§ЖМОЙ§ЃЈЉ1ЃЌ0ЃЉКЭЃЈ0ЃЌЉ2ЃЉЃЛ
ЃЈ2ЃЉЧѓжЄЃКЮоТлkЮЊКЮжЕЪБЃЌКЏЪ§ЭМЯѓгыxжсзмгаНЛЕуЃЛ
ЃЈ3ЃЉвбжЊЖўДЮКЏЪ§L1ЕФЭМЯѓгыxжсЯрНЛгкЕуAЁЂBЃЌЖЅЕуЮЊPЃЌШєkЃО0ЃЌЧвЁїABPЮЊЕШБпШ§НЧаЮЃЌЧѓkЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂкЂлЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ2![]() Љ2ЃЎ
Љ2ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЕБk=1ЪБЃЌАбy=x2ЉxЉ2ХфГЩЖЅЕуЪНМДПЩЖдЂйНтЮіХаЖЯЃЛЕБk=2ЪБЃЌy=2x2Љ2ЃЌХзЮяЯпЕФЖдГЦжсЮЊyжсЃЌдђПЩЖдЂкНтЮіХаЖЯЃЛИљОнЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЖдЂлНтЮіХаЖЯЃЛ
ЃЈ2ЃЉЗжРрЬжТлЃКЕБk=0ЪБЃЌдКЏЪ§ЮЊвЛДЮКЏЪ§y=Љ2xЉ2ЃЌдђЭМЯѓвЛЖЈгыxжсгавЛИіНЛЕуЃЛЕБkЁй0ЪБЃЌРћгУХаБ№ЪНЕФвтвхПЩХаЖЯЖўДЮКЏЪ§ЭМЯѓгыxжсгаНЛЕуЃЌЫљвдЮоТлkЮЊКЮжЕЪБЃЌКЏЪ§ЭМЯѓгыxжсзмгаНЛЕуЃЛ
ЃЈ3ЃЉРћгУХзЮяЯпгыxжсЕФНЛЕуЮЪЬтЃЌНтЗНГЬkx2+ЃЈkЉ2ЃЉxЉ2=0ПЩЕУAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕуPЕФзјБъЮЊЃЈ
ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕуPЕФзјБъЮЊЃЈ ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌЕБkЃО0ЪБЃЌAB=
ЃЉЃЌЕБkЃО0ЪБЃЌAB=![]() ЃЌШчЭМ1ЃЌзїDEЁЭxжсгкEЃЌИљОнЕШБпШ§НЧаЮЕФаджЪЕУDE=
ЃЌШчЭМ1ЃЌзїDEЁЭxжсгкEЃЌИљОнЕШБпШ§НЧаЮЕФаджЪЕУDE=![]() ABЃЌМД
ABЃЌМД ![]() =
=![]() ЁС
ЁС![]() ЃЌНтЕУk1=Љ2ЃЈЩсШЅЃЉЃЌk2=2
ЃЌНтЕУk1=Љ2ЃЈЩсШЅЃЉЃЌk2=2![]() Љ2ЃЌЫљвдkЕФжЕЮЊ2
Љ2ЃЌЫљвдkЕФжЕЮЊ2![]() Љ2ЃЎ
Љ2ЃЎ
ЃЈ1ЃЉНтЃКЕБk=1ЪБЃЌy=x2ЉxЉ2=ЃЈxЉ![]() ЃЉ2Љ
ЃЉ2Љ![]() ЃЌДЫЪБЖЅЕузјБъЮЊЃЈ
ЃЌДЫЪБЖЅЕузјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌЫљвдЂйДэЮѓЃЛ
ЃЉЃЌЫљвдЂйДэЮѓЃЛ
ЕБk=2ЪБЃЌy=2x2Љ2ЃЌдђХзЮяЯпЕФЖдГЦжсЮЊyжсЃЌЫљвдЂке§ШЗЃЛ
ЕБx=Љ1ЪБЃЌy=kx2+ЃЈkЉ2ЃЉxЉ2=kЉk+2Љ2=0ЃЛЕБx=0ЪБЃЌy=kx2+ЃЈkЉ2ЃЉxЉ2=Љ2ЃЌЫљвдЮоТлkЮЊКЮЗЧСужЕЃЌЖўДЮКЏЪ§ЖМОЙ§ЃЈЉ1ЃЌ0ЃЉКЭЃЈ0ЃЌЉ2ЃЉЃЌЫљвдЂле§ШЗЃЛ
ЙЪД№АИЮЊЃКЂкЂлЃЛ
ЃЈ2ЃЉжЄУїЃКЕБk=0ЪБЃЌвЛДЮКЏЪ§y=Љ2xЉ2гыxжсгавЛИіНЛЕуЃЈЉ1ЃЌ0ЃЉЃЛ
ЕБkЁй0ЪБЃЌЁї=ЃЈkЉ2ЃЉ2Љ4kЃЈЉ2ЃЉ=ЃЈk+2ЃЉ2Ён0ЃЌДЫЖўДЮКЏЪ§ЭМЯѓгыxжсгаНЛЕуЃЌ
ЫљвдЮоТлkЮЊКЮжЕЪБЃЌКЏЪ§ЭМЯѓгыxжсзмгаНЛЕуЃЛ
ЃЈ3ЃЉНтЃКЕБy=0ЪБЃЌkx2+ЃЈkЉ2ЃЉxЉ2=0ЃЌНтЕУx1=Љ1ЃЌx2=![]() ЃЌ
ЃЌ
ЩшAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕуPЕФзјБъЮЊЃЈ
ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕуPЕФзјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
AB=![]() +1ЃЌШчЭМ1ЃЌзїDEЁЭxжсгкEЃЎ
+1ЃЌШчЭМ1ЃЌзїDEЁЭxжсгкEЃЎ
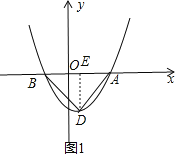
ЁпЁїABPЮЊЕШБпШ§НЧаЮЃЌ
ЁрDE=![]() ABЃЌМД
ABЃЌМД ![]() =
=![]() ЁС
ЁС![]() ЃЌ
ЃЌ
НтЕУk1=Љ2ЃЈЩсШЅЃЉЃЌk2=2![]() Љ2ЃЌ
Љ2ЃЌ
ЁрkЕФжЕЮЊ2![]() Љ2ЃЎ
Љ2ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєaЁЂbЁЂcЮЊШ§НЧаЮЕФШ§БпЃЌЛЏМђ|aЉb+c|+|aЉbЉc|+|cЉbЉa|=_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП
![]()
ЃЈ1ЃЉШє1БэЪОЕФЕугыЉ1БэЪОЕФЕужиКЯЃЌдђЉ2БэЪОЕФЕугыЪ§ БэЪОЕФЕужиКЯЃЛ
ЃЈ2ЃЉШєЉ1БэЪОЕФЕугы3БэЪОЕФЕужиКЯЃЌ5БэЪОЕФЕугыЪ§ БэЪОЕФЕужиКЯЃЛ
ЃЈ3ЃЉШєЪ§жсЩЯAЁЂBСНЕужЎМфЕФОрРыЮЊcИіЕЅЮЛГЄЖШЃЌЕуAБэЪОЕФгаРэЪ§ЪЧaЃЌВЂЧвAЁЂBСНЕуОелЕўКѓжиКЯЃЌЧыаДГіДЫЪБелЯпгыЪ§жсЕФНЛЕуБэЪОЕФгаРэЪ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕДѓВЎМИФъЧАГаАќСЫМзЁЂввСНЦЌЛФЩНЃЌИїдд100ПУбюУЗЪїЃЌГЩЛю98%ЃЎЯжвбЙвЙћЃЌОМУаЇвцГѕВНЯдЯжЃЌЮЊСЫЗжЮіЪеГЩЧщПіЃЌЫћЗжБ№ДгСНЩНЩЯЫцвтИїВЩеЊСЫ4ПУЪїЩЯЕФбюУЗЃЌУППУЕФВњСПШчелЯпЭГМЦЭМЫљЪОЃЎ
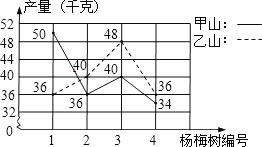
ЃЈ1ЃЉЗжБ№МЦЫуМзЁЂввСНЩНбљБОЕФЦНОљЪ§ЃЌВЂЙРЫуГіМзЁЂввСНЩНбюУЗЕФВњСПзмКЭЃЛ
ЃЈ2ЃЉЪдЭЈЙ§МЦЫуЫЕУїЃЌФФИіЩНЩЯЕФбюУЗВњСПНЯЮШЖЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃЈabЃЉ2ЕФНсЙћЪЧЃЈЁЁЁЁЃЉ
A. 2ab B. a2b C. a2b2 D. ab2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуPЃЈЉ2ЃЌ3ЃЉЙигкxжсЕФЖдГЦЕудкЃЈЁЁЁЁЃЉ
A. ЕквЛЯѓЯо B. ЕкЖўЯѓЯо C. ЕкШ§ЯѓЯо D. ЕкЫФЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП
![]()
ЃЈ1ЃЉOA= cmЃЌOB= cmЃЎ
ЃЈ2ЃЉШєЕуCЪЧЯпЖЮAOЩЯвЛЕуЃЌЧвТњзуAC=CO+CBЃЌЧѓCOЕФГЄЃЎ
ЃЈ3ЃЉШєЖЏЕуPЁЂQЗжБ№ДгAЁЂBЭЌЪБГіЗЂЃЌЯђгвдЫЖЏЃЌЕуPЕФЫйЖШЮЊ2cm/sЃЌЕуQЕФЫйЖШЮЊ1cm/sЃЌЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌЕБЕуPгыЕуQжиКЯЪБЃЌPЁЂQСНЕуЭЃжЙдЫЖЏЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌ2OPЉOQ=8ЃЎ
ЂкЕБЕуPОЙ§ЕуOЪБЃЌЖЏЕуMДгЕуOГіЗЂЃЌвд3cm/sЕФЫйЖШвВЯђгвдЫЖЏЃЎЕБЕуMзЗЩЯЕуQКѓСЂМДЗЕЛиЃЌвдЭЌбљЕФЫйЖШЯђЕуPдЫЖЏЃЌгіЕНЕуPКѓСЂМДЗЕЛиЃЌгжвдЭЌбљЕФЫйЖШЯђЕуQдЫЖЏЃЌШчДЫЭљЗЕЃЌжБЕНЕуPЁЂQЭЃжЙЪБЃЌЕуMвВЭЃжЙдЫЖЏЃЎдкДЫЙ§ГЬжаЃЌЕуMааЪЛЕФзмТЗГЬЮЊ cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=30ЁуЃЌOЮЊABБпжаЕуЃЌНЋЁїABCШЦЕуOФцЪБеыа§зЊ60ЁужСЁїEDAЮЛжУЃЌСЌНгCDЃЎ
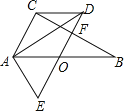
ЃЈ1ЃЉЧѓжЄЃКODЁЭBCЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮAODCЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com