
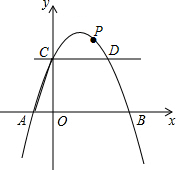
 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.分析 (1)利用待定系数法即可解决问题;
(2)分P在对称轴左右两侧讨论即可;
(3)分点P在点D的上方或下方两种情形讨论即可解决问题.
(4)以A、C、M、P为顶点的四边形是平行四边形有四种情形,分别求解即可.
解答 解:(1)把A(-1,0),B(5,0)代入y=-$\frac{1}{2}$x2+bx+c可得
$\left\{\begin{array}{l}{-\frac{1}{2}-b+c=0}\\{-\frac{1}{2}×{5}^{2}+5b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=\frac{5}{2}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$.
(2)∵抛物线的解析式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$的对称轴x=2,
当点P在对称轴左侧时,如图1中,2-m=1,m=1.
当点P在对称轴右侧时,如图2中,m-2=1,m=3.
(3)过点P作PE⊥CD于点E.
当0<m<2时,如图3中,S=$\frac{1}{2}$×4×(-$\frac{1}{2}$m2+2m+$\frac{5}{2}$-$\frac{5}{2}$)+$\frac{1}{2}$×4×$\frac{5}{2}$=-m2+4m+5.
当m>4时,S=$\frac{1}{2}$×4×($\frac{5}{2}$+$\frac{1}{2}$m2-2m-$\frac{5}{2}$)+$\frac{1}{2}$m×$\frac{5}{2}$=m2-$\frac{11}{4}$m.
(4)①如图5中,当P1与D重合时,四边形ACDM1是平行四边形,易知AM1=CD=4,∴M1(3,0).
②如图6中,当四边形ACM2P2是平行四边形时,作P2H⊥x轴于H.
由△ACO≌△M2P2H,可得P2H=OC=$\frac{5}{2}$,M2H=OA=1,
当y=-$\frac{5}{2}$时,-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=-$\frac{5}{2}$,解得x=2±$\sqrt{14}$,
∴OH=2+$\sqrt{14}$,M2(3+$\sqrt{14}$,0).
③如图7中,当AC是平行四边形DCM3A的对角线时,易知M3(-5,0).
④如图8中,当四边形ACM4P4是平行四边形时,同法可得M4(3-$\sqrt{14}$,0).
点M的坐标为(3,0)或(3+$\sqrt{14}$,0)或(-5,0)或(3-$\sqrt{14}$,0).
点评 本题考查二次函数综合题、平行四边形的判定和性质、四边形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | (2,2) | B. | (-4,2) | C. | (-1,5) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.
如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.
已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
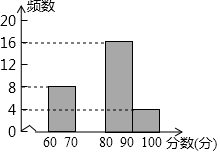 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.| 分数段 (分数为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x<90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com