
【题目】如图,点![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数)的图象的交点.过点
为常数)的图象的交点.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
(1)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() (
(![]() 为常数)的图象于点
为常数)的图象于点![]() ,交垂线
,交垂线![]() 于点
于点![]() .若
.若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
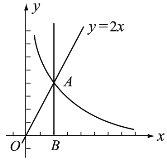
【答案】(1)A(2,4);m=9;(2)6<x1+x2+x3≤7
【解析】
(1)由点A在正比例函数y=2x的图象上,可得点A的坐标为(2,4),再根据点A在反比例函数![]() 的图象上,即可得出m的值;
的图象上,即可得出m的值;
(2)依据x2<x3<x1,结合函数的图象,即可写出x1+x2+x3的取值范围.
解:(1)由题意得,可知点A的横坐标是2,
由点A在正比例函数y=2x的图象上,
∴点A的坐标为(2,4),
又∵点A在反比例函数![]() 的图象上,
的图象上,
∴4=![]() ,
,
即m=9;
(2)∵过点P(0,n)作平行于x轴的直线,交直线y=2x于点C(x1,y1),交反比例函数![]() (m为常数)的图象于点D(x2,y2),交垂线AB于点E(x3,y3),而x2<x3<x1,
(m为常数)的图象于点D(x2,y2),交垂线AB于点E(x3,y3),而x2<x3<x1,
∴4<n≤8,
∵当n=4时,x1+x2+x3=2+2+2=6;当n=8时,x1+x2+x3=4+1+2=7,
∴6<x1+x2+x3≤7.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
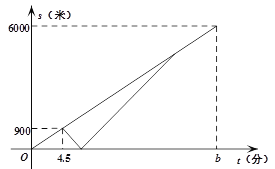
【题目】周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
(1)求a、b的值.
(2)求甲追上乙时,距学校的路程.
(3)当两人相距500米时,直接写出t的值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
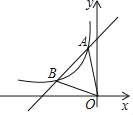
【题目】如图,曲线l是由函数y=![]() 在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A (m,6),B (﹣6,n),则△OAB的面积为_____.
在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A (m,6),B (﹣6,n),则△OAB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
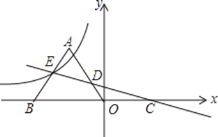
【题目】如图,![]() 为等腰直角三角形,斜边
为等腰直角三角形,斜边![]() 边在
边在![]() 负半轴上,一次函数
负半轴上,一次函数![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,反比例函数
点,反比例函数![]() 的图象的一支过
的图象的一支过![]() 点,若
点,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.-3D.-4
C.-3D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
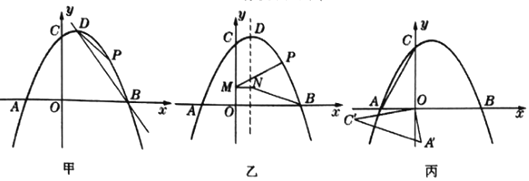
【题目】如图甲所示,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为该抛物线的顶点.
为该抛物线的顶点.
(1)如图甲,点![]() 为抛物线上
为抛物线上![]() ,
,![]() 两点间的一动点,连接
两点间的一动点,连接![]() ,
,![]() ,当
,当![]() 面积最大时,在对称轴上有一动点
面积最大时,在对称轴上有一动点![]() ,如图乙所示,过点
,如图乙所示,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
(2)如图丙所示,将![]() 绕着点
绕着点![]() 旋转,得到
旋转,得到![]() ,在旋转过程中,是否存在某个时刻使以点
,在旋转过程中,是否存在某个时刻使以点![]() 为顶点的三角形为以
为顶点的三角形为以![]() 为腰的等腰三角形,如果存在,请直接写出此时点
为腰的等腰三角形,如果存在,请直接写出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
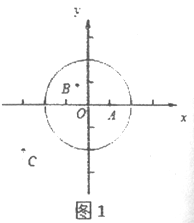
A(1,0)的距离跨度______________;
B(-![]() ,
, ![]() )的距离跨度____________;
)的距离跨度____________;
C(-3,-2)的距离跨度____________;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是______________.
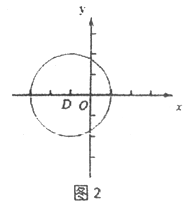
(2)如图2,在平面直角坐标系xOy中,图形G2为以D(-1,0)为圆心,2为半径的圆,直线y=k(x-1)上存在到G2的距离跨度为2的点,求k的取值范围.
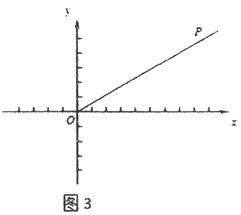
(3)如图3,在平面直角坐标系xOy中,射线OP:y=![]() x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
x(x≥0),⊙E是以3为半径的圆,且圆心E在x轴上运动,若射线OP上存在点到⊙E的距离跨度为2,求出圆心E的横坐标xE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
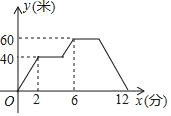
【题目】小明在练习操控航拍无人机,该型号无人机在上升和下落时的速度相同,设无人机的飞行高度为y(米),小明操控无人飞机的时间为x(分),y与x之间的函数图象如图所示.
(1)无人机上升的速度为 米/分,无人机在40米的高度上飞行了 分.
(2)求无人机下落过程中,y与x之间的函数关系式.
(3)求无人机距地面的高度为50米时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
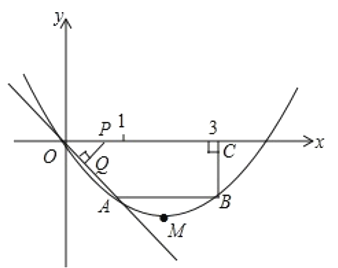
【题目】在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,-1),B(3,-1),动点P从O点出发,沿x轴正方向以3个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0 < t < ![]() ),ΔOPQ与四边形OABC重叠的面积为S.
),ΔOPQ与四边形OABC重叠的面积为S.
(1)求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标;
(2)用含t的代数式表示P、Q两点的坐标;
(3)将ΔOPQ绕P点逆时针旋转90°,是否存在t,使得ΔOPQ的顶点O或Q落在抛物线上?若存在,直接写出t的值;若不存在,请说明理由;
(4)求S与t的函数解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两地相距
两地相距![]() ,甲、乙两人都由
,甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]()
![]() .
.
(1)根据题意,填写表格:
时间 与 | 0.5 | 1.8 | |
甲与 | 5 | 20 | |
乙与 | 0 | 12 |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() .写出
.写出![]() ,
,![]() 关于
关于![]() 的表达式;
的表达式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com