
分析 作圆,求出半径和PC的长度,判出点D只有在CP上时CD最短,CD=CP-DP求解.
解答 解:作圆,使∠ADB=60°,设圆心为P,连结PA、PB、PC,PE⊥AB于E,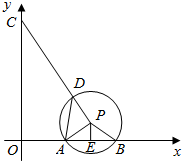 如图所示:
如图所示:
∵A($\sqrt{3}$,0)、B(3$\sqrt{3}$,0),
∴E(2$\sqrt{3}$,0)
又∠ADB=60°,
∴∠APB=120°,
∴PE=1,PA=2PE=2,
∴P(2$\sqrt{3}$,1),
∵C(0,5),
∴PC=$\sqrt{(2\sqrt{3})^{2}+(5-1)^{2}}$=2$\sqrt{7}$,
又∵PD=PA=2,
∴只有点D在线段PC上时,CD最短(点D在别的位置时构成△CDP)
∴CD最小值为:2$\sqrt{7}$-2.
故答案为:2$\sqrt{7}$-2.
点评 本题主要考查坐标与图形的性质,圆周角定理及勾股定理,解决本题的关键是判出点D只有在CP上时CD最短.


科目:初中数学 来源: 题型:选择题
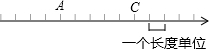 如图,数轴上的点A,C对应的有理数都是整数,若点A对应的有理数为a,点C对应的有理数为c,且c-2a=6,则A点表示的数是( )
如图,数轴上的点A,C对应的有理数都是整数,若点A对应的有理数为a,点C对应的有理数为c,且c-2a=6,则A点表示的数是( )| A. | -1 | B. | -5 | C. | 0 | D. | -21 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
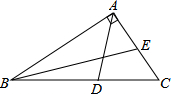 如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:
如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com