
【题目】端午节放假期间,某学校计划租用![]() 辆客车送
辆客车送![]() 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
甲种客车 | 乙种客车 | |
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
(1)求出![]() (元)与
(元)与![]() (辆)之间函数关系式;
(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
【答案】(1)![]() ;(2)
;(2)![]() ,且
,且![]() 为整数;(3)租用甲种客车
为整数;(3)租用甲种客车![]() 辆,租用乙种客车
辆,租用乙种客车![]() 辆,所需的费用最低,最低费用
辆,所需的费用最低,最低费用![]() 元.
元.
【解析】
(1)根据租用甲种客车x辆,则租用乙种客车(6-x)辆,进而表示出总租金即可.
(2)由实际生活意义确定自变量的取值范围.
(3)由题意可列出一元一次不等式方程组.由此推出y随x的增大而增大.
解:(1)设租用甲种客车![]() 辆,则租用乙种客车
辆,则租用乙种客车![]() 辆,
辆,
由题意可得出:![]() ;
;
(2)由![]() 得:
得:![]() .
.
又![]() ,
,
![]()
![]() 的取值范围是:
的取值范围是:![]() ,且
,且![]() 为整数;
为整数;
(3)![]() ,且
,且![]() 为整数,
为整数,
![]() 取
取![]() 或
或![]() 或
或![]()
![]() 中
中![]()
![]() 随
随![]() 的增大而增大
的增大而增大
![]() 当
当![]() 时,
时,![]() 的值最小.
的值最小.
其最小值![]() 元.
元.
则租用甲种客车![]() 辆,租用乙种客车
辆,租用乙种客车![]() 辆,所需的费用最低,最低费用
辆,所需的费用最低,最低费用![]() 元.
元.
故答案为:(1)![]() ;(2)
;(2)![]() ,且
,且![]() 为整数;(3)租用甲种客车
为整数;(3)租用甲种客车![]() 辆,租用乙种客车
辆,租用乙种客车![]() 辆,所需的费用最低,最低费用
辆,所需的费用最低,最低费用![]() 元.
元.


科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
![]()
若n=26,则第2019次“C运算”的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于![]() 小时,小明为了解本班学生参加户外活动的情况,特进行了问卷调查.
小时,小明为了解本班学生参加户外活动的情况,特进行了问卷调查.
(1)在进行问卷调查时有如下步骤,按顺序排列为________(填序号).
①发问卷,让被调查人填写;②设计问卷;③对问卷的数据进行收集与整理;
④收回问卷;⑤得出结论.
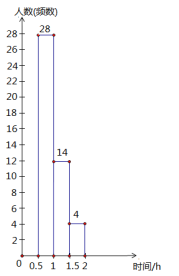
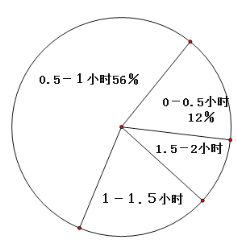
(2)小明根据调查结果,就本班学生每天参加户外活动的平均时间绘制了以下两幅不完整的统计图(图中![]() 表示大于等于
表示大于等于![]() 同时小于
同时小于![]() ,图中类似的记号均表示这一含义),请你根据图中提供的信息解答下列问题:
,图中类似的记号均表示这一含义),请你根据图中提供的信息解答下列问题:
①在这次调查中共调查了多少名学生?
②通过计算补全频数分布直方图;
③请你根据以上统计结果,就学生参加户外活动情况提出建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2 
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 上的一动点(不与点
上的一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 填空:①当
填空:①当![]() ________时,四边形
________时,四边形![]() 是矩形;②当
是矩形;②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
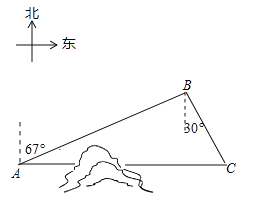
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
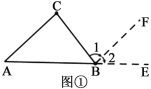
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
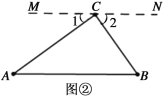
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
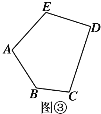
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)数学小组遇到这样一个问题:若a,b均不为零,求![]() 的值.
的值.
请补充以下解答过程(直接填空)
①当两个字母a,b中有2个正,0个负时,x= ;②当两个字母a,b中有1个正,1个负时,x= ;③当两个字母a,b中有0个正,2个负时,x= ;综上,当a,b均不为零,求x的值为 .
(2)请仿照解答过程完成下列问题:
①若a,b,c均不为零,求![]() 的值.
的值.
②若a,b,c均不为零,且a+b+c=0,直接写出代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com