
 如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O运动到线段AB的延长线上或直线AB外,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析,并说明理由.
如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O运动到线段AB的延长线上或直线AB外,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析,并说明理由.  夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
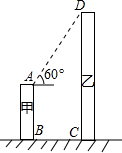 (2013•呼伦贝尔)如图,线段AB、DC分别表示甲乙两座建筑物的高,AB⊥BC,DC⊥BC,两建筑物的水平距离BC为30米,若甲建筑物的高AB=28米,在点A处观察乙建筑物顶部D的仰角为60°,求乙建筑物的高度 (结果保留1位小数,
(2013•呼伦贝尔)如图,线段AB、DC分别表示甲乙两座建筑物的高,AB⊥BC,DC⊥BC,两建筑物的水平距离BC为30米,若甲建筑物的高AB=28米,在点A处观察乙建筑物顶部D的仰角为60°,求乙建筑物的高度 (结果保留1位小数,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
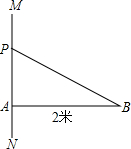 如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).
如图,线段AB长为2米,AB⊥MN,垂足为A,一动点P从点A出发,以1米/秒的速度向射线AM方向移动.设移动的时间为x(秒).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com