
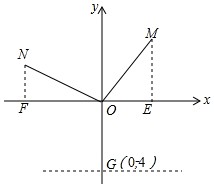
 如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.
如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.分析 (1)作NF⊥x轴于N,ME⊥x轴于E,则∠NFO=∠OEM=90°,先判定△ONF≌△MOE(ASA),再根据M(2,3),即可得出OE=NF=2,ME=FO=3,即可得到N(-3,2);
(2)延长NF到N',使N'F=NF,则N、N'关于x轴的对称.连接N'M交x轴于P,过N'作x轴的平行线,与ME的延长线交于C,构造等腰直角三角形,得出PF=FN'=2,进而得出OP=3-2=1,即可得到P(-1,0);
(3)根据N(-3,2),M(2,3),G(0,-4),可得N到l的距离是6,M到l的距离是7,都大于$\sqrt{26}$,进而得出不存在以QM、QN为底边的等腰三角形.再作MN的中垂线,交l于点Q,则MQ=NQ,即△MNQ是等腰三角形,进而得到存在唯一点Q满足条件.
解答  解:(1)如图所示,作NF⊥x轴于N,ME⊥x轴于E,则∠NFO=∠OEM=90°.
解:(1)如图所示,作NF⊥x轴于N,ME⊥x轴于E,则∠NFO=∠OEM=90°.
∵ON⊥OM,
∴∠NOF+∠MOE=90°,
又∠M+∠MOE=90°,
∴∠M=∠NOF,
在Rt△ONF和Rt△MOE中,
$\left\{\begin{array}{l}{∠M=∠NOF}\\{ON=OM}\\{∠NFO=∠OEM}\end{array}\right.$,
∴△ONF≌△MOE(ASA),
又M(2,3),
∴OE=NF=2,ME=FO=3,
∴N(-3,2);
(2)延长NF到N',使N'F=NF,则N、N'关于x轴的对称.
连接N'M交x轴于P,过N'作x轴的平行线,与ME的延长线交于C.
∵CM=CN'=3+2=5,∠C=90°,
∴∠MN'C=∠CMN'=45°,
∵N'C∥x轴,MC∥y轴,
∴∠PN'F=∠N'PF=45°,
∴PF=FN'=2,
∴OP=3-2=1,
∴P(-1,0);
(3)在l上存在1个点Q.
∵N(-3,2),M(2,3),G(0,-4),
∴N到l的距离是6,M到l的距离是7,都大于$\sqrt{26}$,
∴不存在以QM、QN为底边的等腰三角形.
作MN的中垂线,交l于点Q,则MQ=NQ,即△MNQ是等腰三角形,
∴存在唯一点Q满足条件.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质以及轴对称的性质的综合应用,解决问题的关键是作辅助线构造全等三角形以及等腰直角三角形,根据全等三角形的对应边相等得出结论.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:填空题
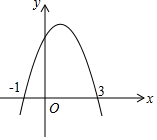 如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)(1)(2)(3).
如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)(1)(2)(3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
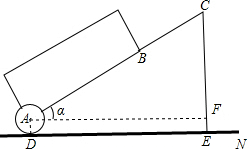 拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).
拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com