
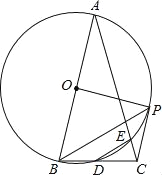
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
【答案】(1)BD=DC;理由见解析;(2)90°;(3)证明见解析;
【解析】
(1)连接AD,由圆周角定理可知∠ADB=90°,再由AB=AC可知△ABC是等腰三角形,故BD=DC;
(2)由于AD是等腰三角形ABC底边上的中线,所以∠BAD=∠CAD,故![]() =
=![]() ,进而可得出BD=DE,故BD=DE=DC,所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
,进而可得出BD=DE,故BD=DE=DC,所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
(3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°在Rt△AOG中,由∠OAG=30°,可知![]() =
=![]() ,由于
,由于![]() =
=![]() =
=![]() ,所以
,所以![]() =
=![]() ,
,![]() =
=![]() ,再根据∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,故可得出CP是 ⊙O的切线.
,再根据∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,故可得出CP是 ⊙O的切线.
解:(1)BD=DC.理由如下:连接AD,
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
(2)∵AD是等腰△ABC底边上的中线,
∴∠BAD=∠CAD,
∴![]() =
=![]() ,
,
∴BD=DE.
∴BD=DE=DC,
∴∠DEC=∠DCE,
△ABC中,AB=AC,∠A=30°,
∴∠DCE=∠ABC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠DEC=75°,
∴∠EDC=180°﹣75°﹣75°=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC﹣∠PBC=75°﹣30°=45°,
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°;
(3)设OP交AC于点G,如图,则∠AOG=∠BOP=90°,
在Rt△AOG中,∠OAG=30°,
∴![]() =
=![]() ,
,
又∵![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵∠AGO=∠CGP,
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴OP⊥PC,
∴CP是⊙O的切线;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
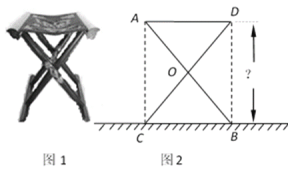
【题目】某大学计划为新生配备如图1所示的折叠椅.图2中的正方形ACBD是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.若正方形ACBD的面积为[9(2x-3y)2+12(2x-3y) (x+4y) +4(x+4y)2](米2)(x>y),你能求出这种折叠椅张开后的高度吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,相向而行,速度都为
同时出发,相向而行,速度都为![]() .以
.以![]() 为一边向上作正方形
为一边向上作正方形![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,单位:
,单位:![]() ,正方形
,正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() .
.
![]() 当
当![]() 时,点
时,点![]() 与点
与点![]() 重合.
重合.
![]() 当
当![]() 时,点
时,点![]() 在
在![]() 上.
上.
![]() 当点
当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,求
两点)时,求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
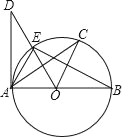
【题目】如图,AB是⊙D的直径,AD切⊙D于点A,EC=CB.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC.一定正确的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
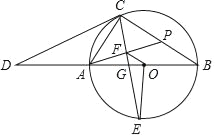
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
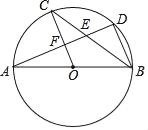
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=AC=20 cm.动点P,Q分别从A,B两点同时出发,沿三角形的边匀速运动.已知点P,点Q的速度都是2 cm/s,当点P第一次到达B点时,P,Q两点同时停止运动.设点P的运动时间为t(s).
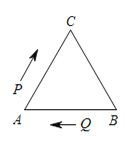
(1)∠A=______度;
(2)当0<t<10,且△APQ为直角三角形时,求t的值;
(3)当△APQ为等边三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提倡绿色出行,某公司在我区![]() 、
、![]() 两个街区分别投放了一批“共享汽车”,“共享汽车”有甲、乙不同款型.
两个街区分别投放了一批“共享汽车”,“共享汽车”有甲、乙不同款型.
(1)该公司在我区![]() 街区早期试点时共投放甲、乙两种型号的“共享汽车”各20辆,投放成本共计划110万,其中甲型汽车的成本单价比乙型汽车少0.5万元,求甲、乙两型“共享汽车”的单价各是多少?
街区早期试点时共投放甲、乙两种型号的“共享汽车”各20辆,投放成本共计划110万,其中甲型汽车的成本单价比乙型汽车少0.5万元,求甲、乙两型“共享汽车”的单价各是多少?
(2)该公司采取了如下的投放方式: ![]() 街区每2000人投放
街区每2000人投放![]() 辆“共享汽车”,
辆“共享汽车”,![]() 街区每2000人投放
街区每2000人投放![]() 辆“共享汽车”,按照这种设放方式,
辆“共享汽车”,按照这种设放方式,![]() 街区共投放150辆,
街区共投放150辆,![]() 街区共投放120辆,如果两个街区共有6万人,试求
街区共投放120辆,如果两个街区共有6万人,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com