Question

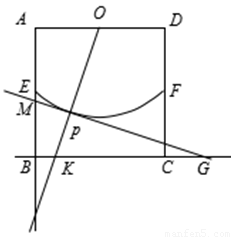
如图在边长为2的正方形ABCD中，E，F，O分别是AB，CD，AD的中点，以O为圆心，以OE为半径画弧EF．P是上的一个动点，连结OP，并延长OP交线段BC于点K，过点P作⊙O的切线，分别交射线AB于点M，交直线BC于点G． 若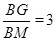，则BK﹦                            ．

 

 

Answer 1

【答案】

,．

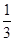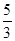【解析】

试题分析：根据MG与⊙O相切得OK⊥MG．设直线OK交AB的延长线于点H，易证∠MGB=∠BHK．根据三角函数定义，tan∠MGB=tan∠BHK=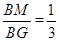 ，从而有AH=3，BH=3BK．因为AB=2，所以BH=1，可求BK．

P为动点，当P接近F点时，本题另有一个解．

试题解析：：（1）若OP的延长线与射线AB的延长线相交，设交点为H．如图1，

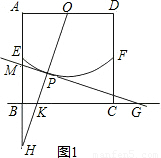
∵MG与⊙O相切，

∴OK⊥MG．

∵∠BKH=∠PKG，

∴∠MGB=∠BHK．

∵，

∴tan∠BHK=．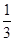

∴AH=3AO=3×1=3，BH=3BK．

∵AB=2，

∴BH=1，

∴BK=．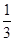

（2）若OP的延长线与射线DC的延长线相交，设交点为H．如图2，

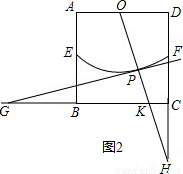
同理可求得BK=．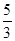

综上所述，本题应填,．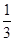

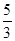考点: 切线的性质．