Question

16．如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB、BA（或它们的延长线）于点E、F，∠EDF=60°，当CE=AF时，如图1小芳同学得出的结论是DE=DF．
（1）继续旋转三角形纸片，当CE≠AF时，如图2小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由；
（2）再次旋转三角形纸片，当点E、F分别在CB、BA的延长线上时，如图3请直接写出DE与DF的数量关系；
（3）连EF，若△DEF的面积为y，CE=x，求y与x的关系式，并指出当x为何值时，y有最小值，最小值是多少？

Answer 1

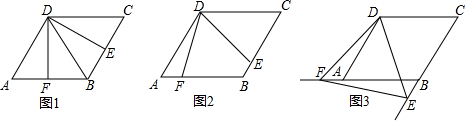
分析 （1）如答图1，连接BD．根据题干条件首先证明∠ADF=∠BDE，然后证明△ADF≌△BDE（ASA），得DF=DE；
（2）如答图2，连接BD．根据题干条件首先证明∠ADF=∠BDE，然后证明△ADF≌△BDE（ASA），得DF=DE；
（3）根据（2）中的△ADF≌△BDE得到：S_△ADF=S_△BDE，AF=BE．所以△DEF的面积转化为：y=S_△BEF+S_△ABD．据此列出y关于x的二次函数，通过求二次函数的最值来求y的最小值．

解答 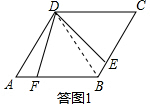解：（1）DF=DE．理由如下：
如答图1，连接BD．
∵四边形ABCD是菱形，
∴AD=AB．
又∵∠DAB=60°，
∴△ABD是等边三角形，
∴AD=BD，∠ADB=60°，
∴∠DBE=∠DAF=60°
∵∠EDF=60°，
∴∠ADF=∠BDE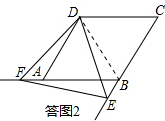．∵在△ADF与△BDE中，$\left\{\begin{array}{l}{∠ADF=∠BDE}\\{AD=BD}\\{∠DAF=∠DBE}\end{array}\right.$，
∴△ADF≌△BDE（ASA），
∴DF=DE；

（2）DF=DE．理由如下：
如答图2，连接BD．∵四边形ABCD是菱形，
∴AD=AB．
又∵∠DAB=60°，
∴△ABD是等边三角形，
∴AD=BD，∠ADB=60°，
∴∠DBE=∠DAF=120°
∵∠EDF=60°，
∴∠ADF=∠BDE．
∵在△ADF与△BDE中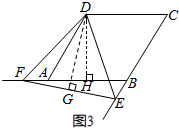，$\left\{\begin{array}{l}{∠ADF=∠BDE}\\{AD=BD}\\{∠DAF=∠DBE}\end{array}\right.$，
∴△ADF≌△BDE（ASA），
∴DF=DE；

（3）由（2）知，DE=DF，又∵∠EDF=60°，
∴△DEF是等边三角形，
∵四边形ABCD是边长为2的菱形，
∴DH=$\sqrt{3}$，
∵BF=CE=x，
∴AF=|x-2|，
∴FH=AF+AH=x-2+1=x-1，
∴DF=$\sqrt{（x-1）^{2}+3}$=$\sqrt{{x}^{2}-2x+4}$，DG=$\frac{\sqrt{3}}{2}$×$\sqrt{{x}^{2}-2x+4}$，
∴y=S_△DEF=$\frac{1}{2}$×EF×DG=$\frac{1}{2}$×$\sqrt{{x}^{2}-2x+4}$×$\frac{\sqrt{3}}{2}$×$\sqrt{{x}^{2}-2x+4}$=$\frac{\sqrt{3}}{4}$（x-1）²+$\frac{3\sqrt{3}}{4}$．
∴当x=1时，y_最小值=$\frac{3\sqrt{3}}{4}$．

点评 本题考查了几何变换综合题，解题过程中，利用了三角形全等的判定与性质，菱形的性质以及等边三角形的判定与性质，对于促进角与角（边与边）相互转换，将未知角转化为已知角（未知边转化为已知边）是关键．