

分析 (1)根据∠MON和∠BOC的度数可以得到∠MON的度数.
(2)根据OC是∠MOB的角平分线,∠BOC=65°可以求得∠BOM的度数,由∠NOM=90°,可得∠BON的度数,从而可得∠CON的度数.
解答 解:(1)∵∠MON=90°,∠BOC=65°,
∴∠MOC=∠MON-∠BOC=90°-65°=25°.
故答案为:25°.
(2)∵∠BOC=65°,OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB-∠MON
=130°-90°
=40°.
∠CON=∠COB-∠BON
=65°-40°
=25°.
点评 本题考查了角的计算和旋转的知识,关键是明确题意,灵活变化,找出所求问题需要的量.


科目:初中数学 来源: 题型:解答题
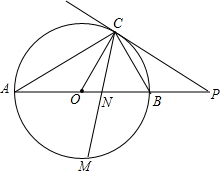 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
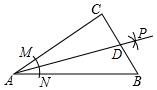 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=2,AB=6,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=2,AB=6,则△ABD的面积是( )| A. | 3 | B. | 6 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
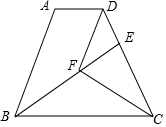 如图,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
如图,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com