
分析 由于二次函数的二次项系数a=1>0,由此可以确定抛物线开口方向,利用y=ax2+bx+c的顶点坐标公式为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是x=-$\frac{b}{2a}$可以确定对称轴,然后即可确定在对称轴的左侧y随x的增大而减小,由此得到x的取值范围.
解答 解:∵y=x2-2x+3,
∴二次函数的二次项系数a=1>0,
∴抛物线开口向上,
∵y=ax2+bx+c的顶点坐标公式为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是x=-$\frac{b}{2a}$,
∴此函数对称轴是x=1,顶点坐标是(1,2),
∴当x<1时,y随x的增大而减小.
故答案为:(1,2),<1.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是直线x=-$\frac{b}{2a}$.当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点. 当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )| A. | $\frac{AE}{ED}=\frac{BE}{EH}$ | B. | $\frac{EH}{EB}=\frac{DH}{CD}$ | C. | $\frac{EG}{BG}=\frac{AE}{BC}$ | D. | $\frac{AG}{FG}=\frac{BG}{GH}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
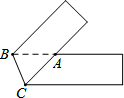 将一张宽为5cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是$\frac{25}{2}$cm2.
将一张宽为5cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是$\frac{25}{2}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
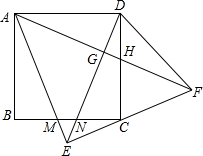 如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.
为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com