
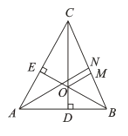
【题目】如图,在△ABC中,CD、BE为高,AN为角平分线,OM平分∠BOC交BC于M.
(1) 若∠BAC=![]() ,求∠BOM;
,求∠BOM;
(2) 求证: OM∥AN.
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于C、D两点,与双曲线
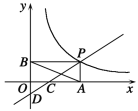
与x轴、y轴分别交于C、D两点,与双曲线![]() 在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
在第一象限内交于点P,过点P作PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,4)且S△DBP=27.
(1)直接写出直线的解析式_____________,双曲线的解析式____________;
(2)设点Q是直线![]() 上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
上的一点,且满足△DOQ的面积是△COD面积的2倍,请求出点Q的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心,2 cm长为半径的圆和AB的位置关系是_________;
(2)以C为圆心,4 cm长为半径的圆和AB的位置关系是_________;
(3)如果以C为圆心的圆和AB相切,则半径长为_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
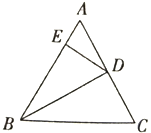
【题目】如图,在等边三角形ABC中,D为AC的中点,![]() ,则和△AED(不包含△AED)相似的三角形有( )
,则和△AED(不包含△AED)相似的三角形有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
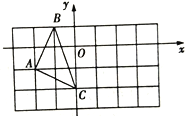
【题目】如图,在平面直角坐标系中,△ABC的三个点坐标分别为A(-2,-1),B(-1,1),C(0,-2).
(1)点B关于坐标原点O对称的点的坐标为____________.
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C1;
(3)以点O为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的相似比为1:2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,①等腰三角形两腰上的高相等;②在空间中,垂直于同一直线的两直线平行;③两条直线被第三条直线所截,内错角相等;④一个角的两边与另一个角的两边分别平行, 则这两个角相等. 其中真命题的个数有 __________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 、
、![]() 与相交于点
与相交于点![]() ,形成了
,形成了![]() 个角.
个角.
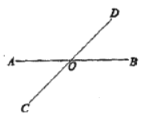
(1)图中,![]() 与
与![]() 有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
(2)图中,![]() 与
与![]() 有一个公共顶点,且
有一个公共顶点,且![]() 的两边分别是
的两边分别是![]() 的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
(3)因为![]() ______________,
______________,![]() ____________所以
____________所以![]() ______
______![]() (填写
(填写![]() 或
或![]() 或
或![]() )理由是____________由此能得到的结论是:对顶角_____________
)理由是____________由此能得到的结论是:对顶角_____________
(4)用您所学知识可得![]() ___________(精确到度).
___________(精确到度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com