
 如图,正方形OABC的边OA、OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA、OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).分析 (1)易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标;
(2)由(1)可求得D的坐标,从而可表示出OD的解析式;
(3)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.容易得到△POE周长等于AO+CO=8,从而解决问题;
解答 解:
(1)如图1,
由题可得:AP=OQ=1×t=t(秒)
∴AO=PQ.
∵四边形OABC是正方形,
∴AO=AB=BC=OC,
∠BAO=∠AOC=∠OCB=∠ABC=90°.
∵DP⊥BP,
∴∠BPD=90°.
∴∠BPA=90°-∠DPQ=∠PDQ.
∵AO=PQ,AO=AB,
∴AB=PQ.
在△BAP和△PQD中,
$\left\{\begin{array}{l}{∠BAP=∠PQD}\\{∠BPA=∠PDQ}\\{AB=PQ}\end{array}\right.$
∴△BAP≌△PQD(AAS).
∴AP=QD,BP=PD.
∵∠BPD=90°,BP=PD,
∴∠PBD=∠PDB=45°.
∵AP=t,
∴DQ=t.
∴点D坐标为(t,t).
故答案为:45°,(t,t).
(2)不变化,
∵D(t,t),
∴点D在直线y=x上,
即直线OD的解析式为y=x;
(3)延长OA到点F,使得AF=CE,连接BF,如图2所示.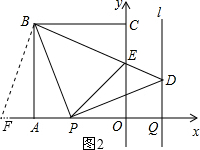
在△FAB和△ECB中,
$\left\{\begin{array}{l}{AB=CB}\\{∠BAF=∠BCE}\\{AF=CE}\end{array}\right.$
∴△FAB≌△ECB.
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP
=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP和△EBP中,
$\left\{\begin{array}{l}{BF=BE}\\{∠FBP=∠EBP}\\{BP=BP}\end{array}\right.$
∴△FBP≌△EBP(SAS).
∴FP=EP.
∵∠EBP=45°,
∴由图1可以得到EP=CE+AP,
∴OP+PE+OE=OP+AP+CE+OE
=AO+CO
=4+4
=8.
∴△POE周长是定值,该定值为8.
点评 本题为一次函数的综合应用,涉及正方形的性质、等腰三角形的性质、全等三角形的性质与判定、勾股定理及分类讨论思想等知识.考查利用基本活动经验解决问题的能力,综合性非常强.熟悉正方形与一个度数为45°的角组成的基本图形(其中角的顶点与正方形的一个顶点重合,角的两边与正方形的两边分别相交)是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:
新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )| A. | (-4,-1) | B. | (-1,-4) | C. | (5,-4) | D. | (-5,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )
如图,甲、乙两所学校,其中男女生情况可见下列统计图,甲学校有1000人,乙有1250人,则( )| A. | 甲校的女生比乙校的女生多 | B. | 甲校的女生比乙校的女生少 | ||
| C. | 甲校与乙校的女生一样多 | D. | 甲校与乙校男生共是2250人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
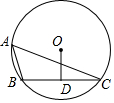 如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )
如图,⊙O的半径长为2,点A、B、C在⊙O上,∠BAC=60°,OD⊥BC于D,则OD的长是( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
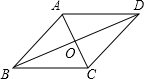 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )| A. | AB=AD | B. | AC=BD | C. | BD平分∠ABC | D. | AC⊥BD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
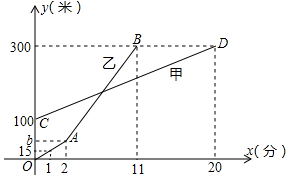 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )| A. | 165m | B. | 160m | C. | 135m | D. | 120m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
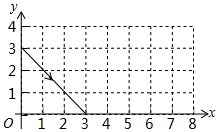 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )| A. | (3,0) | B. | (0,3) | C. | (1,4) | D. | (8,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com