
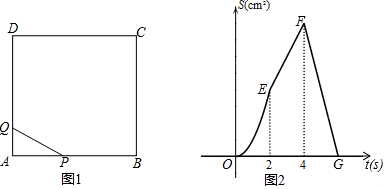
分析 (1)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.求出S的表达式,并确定t的取值范围;
(2)分CP=CQ、PC=PQ、QC=QP三种情况讨论即可确定答案;
(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,求出t的值;
当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,求出t的值.
解答 解:(1)由题意,可知题图2中点E表示点P运动至点B时的情形,
所用时间为2s,则正方形的边长AB=2×2=4cm.
点Q运动至点D所需时间为:4÷1=4s,点P运动至终点D所需时间为12÷2=6s.
因此在FG段内,点Q运动至点D停止运动,点P在线段CD上继续运动,且时间t的取值范围为4≤t≤6.
故S=$\frac{1}{2}$×4×(12-2t)=-4t+24,
∴FG段的函数表达式为S=-4t+24(4≤t≤6).
(2)①若CP=CQ,则DQ=PB,显然不成立
②若PC=PQ,则(4-2t)2+42=5t2,解得${t_1}=-8+4\sqrt{6}$,${t_2}=-8-4\sqrt{6}$(舍去)
③若QC=QP,则(4-t)2+42=5t2,解得t1=2,t2=-4(舍去)
综上所述,当$t=-8+4\sqrt{6}$或t=2时,以C、P、Q为顶点的三角形是等腰三角形.
(3)假设存在这样的t,使PQ将正方形ABCD的面积恰好分成1:3的两部分.
易得正方形ABCD的面积为16.
①当点P在AB上运动时,PQ将正方形ABCD分成△APQ和五边形PBCDQ两部分,
如图1所示,根据题意,得$\frac{1}{2}×2t×t=16×\frac{1}{4}$,解得t=2; 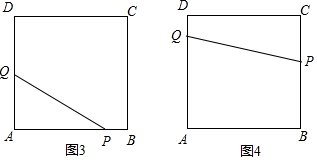
②当点P在BC上运动时,PQ将正方形ABCD分为梯形ABPQ和梯形PCDQ两部分,如图所示.根据题意,得$\frac{1}{2}$(2t-4+t)×4=$\frac{3}{4}$×16,
解得t=$\frac{10}{3}$.
∴存在t=2和t=$\frac{10}{3}$,使PQ将正方形ABCD的面积恰好分成1:3的两部分.
点评 本题是运动型综合题,考查了动点问题的函数图象、菱形的性质、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
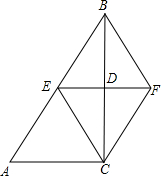 如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件AC=BC,使四边形BECF是正方形.
如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件AC=BC,使四边形BECF是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | i | D. | -i |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com