练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    小明在画出函数y＝2x＋1的图象后发现，当这个图象上的某些点的横坐标取到某些值时，这些点的纵坐标都大于0，则这些点的横坐标x的取值范围是________

    答案：
    解析：

    x＞－


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2010年浙江省金华市初中毕业生学业考试数学试卷 题型：044

    已知点P的坐标为(m，0)，在x轴上存在点Q(不与P点重合)，以PQ为边作正方形PQMN，使点M落在反比例函数y＝－的图像上．小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限．

    (1)如图所示，若反比例函数解析式为y＝－，P点坐标为(1，0)，图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标；(温馨提示：作图时，别忘了用黑色字迹的钢笔或签字笔描黑喔！)M1的坐标是________

    (2)请你通过改变P点坐标，对直线M1M的解析式y﹦kx＋b进行探究可得k﹦________，若点P的坐标为(m，0)时，则b﹦________；

    (3)依据(2)的规律，如果点P的坐标为(6，0)，请你求出点M1和点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2013届江苏省南京市鼓楼区中考二模数学试卷（带解析） 题型：解答题

    【提出问题】
    如图①，在梯形ABCD中，AD//BC，AC、BD交于点E，∠BEC＝n°，若AD＝a，BC＝b，则梯形ABCD的面积最大是多少？
    【探究过程】
    小明提出：可以从特殊情况开始探究，如图②，在梯形ABCD中，AD//BC，AC⊥BD，若AD＝3，BC＝7，则梯形ABCD的面积最大是多少？
    如图③，过点D做DE//AC交BC的延长线于点E，那么梯形ABCD的面积就等于△DBE的面积，求梯形ABCD的面积最大值就是求△DBE的面积最大值．如果设AC＝x，BD＝y，那么S△DBE＝xy．
    以下是几位同学的对话：
    A同学：因为y＝，所以S△DBE＝x，求这个函数的最大值即可．
    B同学：我们知道x2＋y2＝100，借助完全平方公式可求S△DBE＝xy的最大值
    C同学：△DBE是直角三角形，底BE＝10，只要高最大，S△DBE就最大，我们先将所有满足BE＝10的直角△DBE都找出来，然后在其中寻找高最大的△DBE即可．

    （1）请选择A同学或者B同学的方法，完成解题过程．
    （2）请帮C同学在图③中画出所有满足条件的点D，并标出使△DBE面积最大的点D1．（保留作图痕迹，可适当说明画图过程）
    【解决问题】
    根据对特殊情况的探究经验，请在图①中画出面积最大的梯形ABCD的顶点D1，并直接写出梯形ABCD面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏省南京市鼓楼区中考二模数学试卷（解析版） 题型：解答题

    【提出问题】

    如图①，在梯形ABCD中，AD//BC，AC、BD交于点E，∠BEC＝n°，若AD＝a，BC＝b，则梯形ABCD的面积最大是多少？

    【探究过程】

    小明提出：可以从特殊情况开始探究，如图②，在梯形ABCD中，AD//BC，AC⊥BD，若AD＝3，BC＝7，则梯形ABCD的面积最大是多少？

    如图③，过点D做DE//AC交BC的延长线于点E，那么梯形ABCD的面积就等于△DBE的面积，求梯形ABCD的面积最大值就是求△DBE的面积最大值．如果设AC＝x，BD＝y，那么S△DBE＝xy．

    以下是几位同学的对话：

    A同学：因为y＝，所以S△DBE＝x，求这个函数的最大值即可．

    B同学：我们知道x2＋y2＝100，借助完全平方公式可求S△DBE＝xy的最大值

    C同学：△DBE是直角三角形，底BE＝10，只要高最大，S△DBE就最大，我们先将所有满足BE＝10的直角△DBE都找出来，然后在其中寻找高最大的△DBE即可．

    （1）请选择A同学或者B同学的方法，完成解题过程．

    （2）请帮C同学在图③中画出所有满足条件的点D，并标出使△DBE面积最大的点D1．（保留作图痕迹，可适当说明画图过程）

    【解决问题】

    根据对特殊情况的探究经验，请在图①中画出面积最大的梯形ABCD的顶点D1，并直接写出梯形ABCD面积的最大值．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）夜晚，小明在路灯下散步．已知小明身高1.5米，路灯的灯柱高4.5米．

    ①如图1，若小明在相距10米的两路灯AB、CD之间行走（不含两端），他前后的两个影子长分别为FM＝x米，FN＝y米，试求y与x之间的函数关系式，并指出自变量x的取值范围；







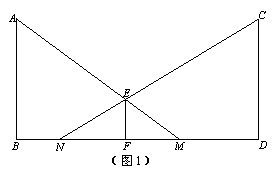
    ②有言道：形影不离．其原意为：人的影子与自己紧密相伴，无法分离．但在灯光下，人的速度与影子的速度却不是一样的！如图2，若小明在灯柱PQ前，朝着影子的方向（如图箭头），以0.8米/秒的速度匀速行走，试求他影子的顶端R在地面上移动的速度．






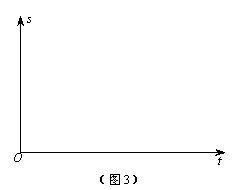
    （2）我们知道，函数图象能直观地刻画因变量与自变量之间的变化关系．相信，大家都听说过龟兔赛跑的故事吧．现有一新版龟兔赛跑的故事：由于兔子上次比赛过后不服气，于是单挑乌龟再来另一场比赛，不过这次路线由乌龟确定……比赛开始，在同一起点出发，按照规定路线，兔子飞驰而出，极速奔跑，直至跑到一条小河边，遥望着河对岸的终点，兔子呆坐在那里，一时不知怎么办．过了许久，乌龟一路跚跚而来，跳入河中，以比在陆地上更快的速度游到对岸，抵达终点，再次获胜．根据新版龟兔赛跑的故事情节，请在同一坐标系内（如图3），画出乌龟、兔子离开终点的距离s与出发时间t的函数图象示意图．（实线表示乌龟，虚线表示兔子）

    查看答案和解析>>

    同步练习册答案