
| 10 |
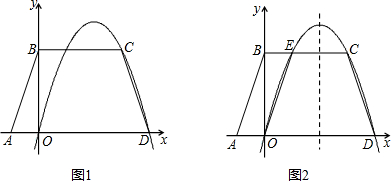
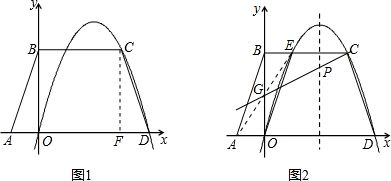 �⣺��1������C��CF��AD��F��
�⣺��1������C��CF��AD��F��| CD2-DF2 |
|
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 3 |
| 7 |
| 3 |
(-1-2)2+(0-
|
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 65 |
| 18 |
| 5 |
| 7 |
| 3 |
| 65 |
| 18 |


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
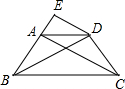
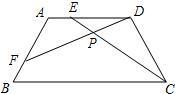 1����ͼ���ڵ�������ABCD�У�AD��BC����B=60�㣬AD=AB����E��F�ֱ���AD��AB�ϣ�AE=BF��DF��CE�ཻ��P�����DPE=
1����ͼ���ڵ�������ABCD�У�AD��BC����B=60�㣬AD=AB����E��F�ֱ���AD��AB�ϣ�AE=BF��DF��CE�ཻ��P�����DPE=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
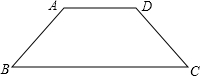
 ��2005•բ������ģ����֪����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC������D��AC��ƽ����DE����BA���ӳ����ڵ�E����֤��
��2005•բ������ģ����֪����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC������D��AC��ƽ����DE����BA���ӳ����ڵ�E����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•�Ϻӿ���ģ�⣩��ͼ���ڵ�������ABCD�У�AD��BC��AB=AD��BC=��
��2013•�Ϻӿ���ģ�⣩��ͼ���ڵ�������ABCD�У�AD��BC��AB=AD��BC=��| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
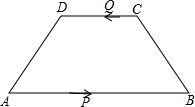 ���У���һ�����˶����յ�ʱ�������˶�����ֹ������P��Qͬʱ�������˶���t�룺
���У���һ�����˶����յ�ʱ�������˶�����ֹ������P��Qͬʱ�������˶���t�룺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���п��ر���04ȫ���п����⼯������ѧ ���ͣ�044
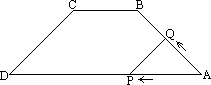
��ͼ���ڵ�������AB�Ρ�CD�У�BC��AD��BC��8��AD��20��AB��DC��10����P��A�������AD�����D�ƶ�����Q��A�������A��B��C��·���ƶ�����PQ��DC����AP��x������λ���߶�PQ�Ҳಿ�ֵ����ΪS��
 ����
����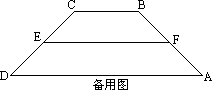
(1)�ֱ��������Qλ��AB��BC��ʱ��S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(2)���߶�PQ������AB�Ρ�CD�ֳ������ȵ�������ʱ��x��ֵ�Ƕ��٣�
(3)��(2)�������£����߶�PQ������AB�Ρ�CD����λ��EF����O�㣬��ôOE��OF�ij�����ʲô��ϵ����������ͼ˵�����ɣ�����һ��̽�������κ�һ�����Σ���һֱ��l����������λ�ߵ��е㲢����ʲô����ʱ��һ����ƽ�����ε������(ֻҪ��˵������������Ҫ֤��)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com