
【题目】计算下列各题
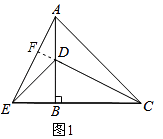
(1)如图1,△ABC和△E中,AB=CB,DB=EB,∠ABC=∠DBE=90°,D点在AB上,连接AE、DC.则AE和CD有什么数量和位置关系? 
(2)类比: 若将图1中的△DBE绕点B逆时针旋转一个锐角,如图2所示,问图2中的线段AE,CD之间的数量和位置关系还成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】
(1)解:AE=CD,AE⊥CD,
理由:延长CD交AE于F,
在△AEB和△CDB中,
∵ 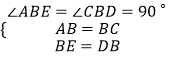 ,
,
∴△AEB≌△CDB(SAS)
∴AE=CD,
∠EAB=∠DCB,
∵∠DCB+∠CDB=90°,
∠ADF=∠CDB,
∴∠ADF+∠DAF=90°,
∴∠AFD=90°,
∴AE⊥CD
(2)解:解:(2)AE=CD,AE⊥CD,
∵∠DBE=∠ABC=90°,
∴∠ABE=∠DBC,
在△AEB和△CDB中, 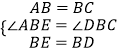
∴△AEB≌△CDB,
∴AE=CD,∠EAB=∠DCB,
∵∠DCB+∠COB=90°,∠AOK=∠COB,
∴∠KOA+∠KAO=90°,
∴∠AKC=90°,
∴AE⊥CD.
【解析】(1)延长CD交AE于K,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,由于∠DCB+∠CDB=90°,于是得到结论;(2)由于∠DBE=∠ABC=90°,得到∠ABE=∠DBC,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,等量代换得到∠KOA+∠KAO=90°,于是得到结论.
【考点精析】掌握旋转的性质是解答本题的根本,需要知道①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (
(![]() )与y轴交于点C,与x轴交于点A(1,0)和点B.
)与y轴交于点C,与x轴交于点A(1,0)和点B.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( ) 
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.0不是正数也不是负数
B.负数是带“—”的数,正数是带有“+”的数
C.非负数是正数或0
D.0是一个特殊的整数,它并不只是表示“没有”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com