
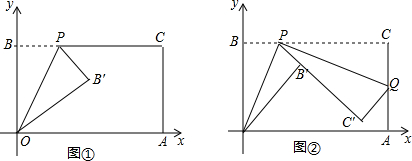
分析 (1)根据题意得,∠OBP=90°,OB=6,在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t,然后利用勾股定理,即可得方程,解此方程即可求得答案;
(2)由△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,可知△OB′P≌△OBP,△QC′P≌△QCP,易证得△OBP∽△PCQ,然后由相似三角形的对应边成比例,即可求得答案;
(3)首先过点P作PE⊥OA于E,易证得△PC′E∽△C′QA,由勾股定理可求得C′A的长,然后利用相似三角形的对应边成比例与m和t的关系,即可求得t的值,得出P点坐标.
解答 解:(1)根据题意,∠OBP=90°,OB=6,
在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t.
∵OP2=OB2+BP2,
即(2t)2=62+t2,
解得:t1=2$\sqrt{3}$,t2=-2$\sqrt{3}$(舍去).
∴点P的坐标为(2$\sqrt{3}$,6);
(2)∵△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,
∴△OB′P≌△OBP,△QC′P≌△QCP,
∴∠OPB′=∠OPB,∠QPC′=∠QPC,
∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°,
∴∠OPB+∠QPC=90°,
∵∠BOP+∠OPB=90°,
∴∠BOP=∠CPQ,
又∵∠OBP=∠C=90°,
∴△OBP∽△PCQ,
∴$\frac{OB}{PC}$=$\frac{BP}{CQ}$,
由题意设BP=t,AQ=m,BC=11,AC=6,则PC=11-t,CQ=6-m.
∴$\frac{6}{11-t}$=$\frac{t}{6-m}$,
∴m=$\frac{1}{6}$t2-$\frac{11}{6}$t+6(0<t<11);
(3)过点P作PE⊥OA于E,如图3,
∴∠PEA=∠QAC′=90°,
∴∠PC′E+∠EPC′=90°,
∵∠PC′E+∠QC′A=90°,
∴∠EPC′=∠QC′A,
∴△PC′E∽△C′QA,
∴$\frac{PE}{AC′}$=$\frac{C′E}{AQ}$,
在△PC′E和△OC′B′中,
$\left\{\begin{array}{l}{∠PEC′=∠OB′C}\\{∠PC′E=∠OC′B′}\\{PE=OB′}\end{array}\right.$,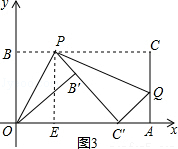
∴△PC′E≌△OC′B′(AAS),
∴PC'=OC'=PC,
∴BP=AC',
∵AC′=PB=t,PE=OB=6,AQ=m,EC′=11-2t,
∴$\frac{6}{t}$=$\frac{11-2t}{m}$,
∵m=$\frac{1}{6}$t2-$\frac{11}{6}$t+6,
∴3t2-22t+36=0,
解得:t1=$\frac{11-\sqrt{13}}{3}$,t2=$\frac{11+\sqrt{13}}{3}$
故点P的坐标为( $\frac{11-\sqrt{3}}{3}$,6)或( $\frac{11+\sqrt{13}}{3}$,6).
点评 本题考查了几何变换综合性题目,用到的知识点有:翻折变换的性质、矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、解一元二次方程等有关的知识点,综合性较强,难度较大.清楚翻折前后的两个图形全等以及熟悉相似三角形的判定与性质是解决本题的关键.


科目:初中数学 来源: 题型:选择题
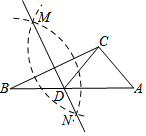 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD. 若CD=AC,∠A=50°,则∠ACB的度数为( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD. 若CD=AC,∠A=50°,则∠ACB的度数为( )| A. | 105° | B. | 100° | C. | 95° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线C1:y1=-x2关于直线x=1对称,可得到抛物线C2.且C1和C2交于点P,顶点分别是点O和点Q.
如图,在平面直角坐标系中,抛物线C1:y1=-x2关于直线x=1对称,可得到抛物线C2.且C1和C2交于点P,顶点分别是点O和点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
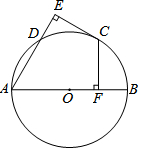 如图,AB是⊙O的直径,C,D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF.
如图,AB是⊙O的直径,C,D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
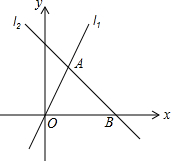 如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).
如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).查看答案和解析>>
科目:初中数学 来源:2017届江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是
A. 摸出的是3个白球 B. 摸出的是3个黑球
C. 摸出的是2个白球、1个黑球 D. 摸出的是2个黑球、1个白球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com