
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).
在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
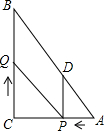 如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点D从点A开始,沿边AB向点B以每秒$\frac{5}{3}$个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,BC=8,AC=6,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点D从点A开始,沿边AB向点B以每秒$\frac{5}{3}$个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.7 | B. | 6.7<x<6.18 | C. | 6.18<x<6.19 | D. | 6.9<x<9.20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com