
 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.分析 (1)要求△PEF的边长,需构造直角三角形,那么就过P作PQ⊥BC于Q.利用∠PFQ的正弦值可求出PF,即△PEF的边长;
(2)由矩形ABCD中,AD∥BC,易得△APH∽△CFH;
(3)猜想:PH-BE=1.利用∠ACB的正切值可求出∠ACB的度数,再由∠PFE=60°,可得出△HFC是等腰三角形,因此就有BE+EF+CF=BE+PH+2FH=3.再把其中FH用PH表示,化简即可.
解答 解:(1)过P作PQ⊥BC于Q.
∵矩形ABCD中,∠B=90°,即AB⊥BC,
又∵AD∥BC,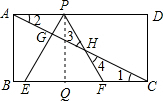 ∴PQ=AB=$\sqrt{3}$,
∴PQ=AB=$\sqrt{3}$,
∵△PEF是等边三角形,
∴∠PFQ=60°.
在Rt△PQF中,PF=$\frac{PQ}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴△PEF的边长为2;
(2)△APH∽△CFH.
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠2,
∵∠3=∠4,
∴△APH∽△CFH;
(3)在Rt△ABC中,AB=$\sqrt{3}$,BC=3,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{3}$,
∴∠ACB=30°,
∵△PEF是等边三角形,
∴∠2=60°,PF=EF=2,
∵∠2=∠1+∠3,
∴∠3=30°,
∴∠1=∠3,
∴FC=FH,
∵PH+FH=2,BE+FC=3-EF=3-2=1,
∴PH-BE=1.
点评 此题属于四边形的综合题.考查了矩形的性质、相似三角形的判定、等边三角形的判定与性质以及勾股定理等知识.注意准确作出辅助线是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.
如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
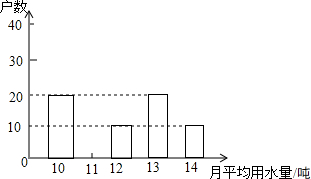 市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解湖南电视台“快乐大本营”栏目的收视率 | |
| B. | 了解一批圆珠笔芯的使用寿命 | |
| C. | 调查一批新型节能灯泡的使用寿命 | |
| D. | 全国人口普查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
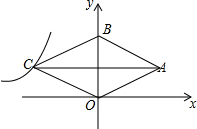 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | 12 | B. | 24 | C. | -12 | D. | -24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
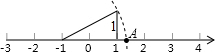 如图所示,数轴上点A所表示的数为a,则a的值是( )
如图所示,数轴上点A所表示的数为a,则a的值是( )| A. | -$\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com