
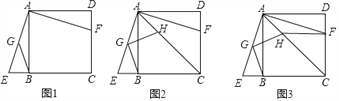
【题目】某数学活动小组在做角的拓展图形练习时,经历了如下过程:

(1)操作发现:点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,如图:将图1中的三角板绕点
的下方,如图:将图1中的三角板绕点![]() 旋转,当直角三角板的
旋转,当直角三角板的![]() 边在
边在![]() 的内部,且恰好平分
的内部,且恰好平分![]() 时,如图2.则下列结论正确的是 (填序号即可).
时,如图2.则下列结论正确的是 (填序号即可).
①![]() ②
②![]() ③
③![]() 平分
平分![]() ④
④![]() 的平分线在直线
的平分线在直线![]() 上
上
(2)数学思考:同学们在操作中发现,当三角板绕点![]() 旋转时,如果直角三角板的
旋转时,如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,请你说明理由;如果直角三角板的
的差不变,请你说明理由;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,请直接写出
的和不变,请直接写出![]() 与
与![]() 的和,不要求说明理由.
的和,不要求说明理由.
(3)类比探索:三角板绕点![]() 继续旋转,当直角三角板的
继续旋转,当直角三角板的![]() 边在
边在![]() 的内部时,如图3,求
的内部时,如图3,求![]() 与
与![]() 相差多少度?为什么?
相差多少度?为什么?
【答案】(1)①②④;(2)如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,理由见解析;如果直角三角板的
的差不变,理由见解析;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,
的和不变,![]() +
+![]() =30°;③30°.
=30°;③30°.
【解析】
(1)利用角平分线的定义结合直角三角板的内角度数即可分别判断得出答案;
(2)当直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方时根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,可得出结果;当直角三角板的
在直线AB的下方时根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,可得出结果;当直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部时,∠COM+∠BON=∠BOC-∠MON,可得出结果;
的内部时,∠COM+∠BON=∠BOC-∠MON,可得出结果;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,然后作差即可.
解:(1)∵![]() ,
,![]() 平分
平分![]() ,∴
,∴![]() ,故①正确;
,故①正确;
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,故②正确;
,故②正确;
∵![]() ,
,![]() ,∴
,∴![]() 不平分
不平分![]() ,故③错误;
,故③错误;
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() 的平分线在直线
的平分线在直线![]() 上,故④正确;
上,故④正确;
故答案为:①②④.
(2)![]() 与
与![]() 的差不变.理由如下:当直角三角板的
的差不变.理由如下:当直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方时,
在直线AB的下方时,
∵∠COM=∠BOC-∠COM=120°-∠BOM,
∠BON=∠MON-∠BOM=90°-∠BOM,
∴∠COM-∠BON=120°-90°=30°;![]() 与
与![]() 的和不变,其和为30°.理由如下:当直角三角板的
的和不变,其和为30°.理由如下:当直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部时,∠COM+∠BON=∠BOC-∠MON=120°-90°=30°.
的内部时,∠COM+∠BON=∠BOC-∠MON=120°-90°=30°.
(3)∵![]() ,
,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,九年级毕业生统一参加理化生实践操作科目考试。根据我市实际情况,市教育局决定:理化生实践考查科目命制24题,分4个试题单元,每个单元内含6道理化生实验操作题。即:物理3题;化学2题;生物1题。小聪与小明是某实验中学九年级的同班同学,在三月份举行的理化生考试中,他们同时抽到同一个试题单元,且每个同学都是同一个试题单元里随机抽取一题。
(1)小聪抽到物理学科科目可能性有多大?
(2)用列表法或树状图,求他俩同时抽到生物的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在精准扶贫中,李师傅在当地政府的扶持下,去年下半年,他开办的桌椅加工厂取得了非常好的经济效益,他决定制作一批课桌捐赠给山区学校:已知制作一张桌子要用一个桌面和4条桌腿,1m3木材可制作20个桌面,或者制作400条桌腿,现有12m3木材,应怎样计划用料才能制作尽可能多的桌子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解.
x﹣8的解.
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个一元一次方程的一次项系数与常数项的差刚好是这个方程的解,则称这个方程为妙解方程.例如:方程![]() 中,
中,![]() ,方程的解为
,方程的解为![]() ,则方程
,则方程![]() 为妙解方程.请根据上述定义解答下列问题:
为妙解方程.请根据上述定义解答下列问题:
(1)方程![]() 是妙解方程吗?试说明理由.
是妙解方程吗?试说明理由.
(2)已知关于![]() 的一元一次方程
的一元一次方程![]() 是妙解方程.求
是妙解方程.求![]() 的值.
的值.
(3)已知关于![]() 的一元一次方程
的一元一次方程![]() 是妙解方程,并且它的解是
是妙解方程,并且它的解是![]() .求代数式
.求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
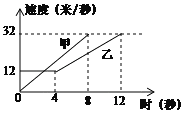
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程![]() =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.
经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程![]() 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com