

分析 根据翻折变换表示出所得图形的面积,再根据各部分图形的面积之和等于正方形的面积减去剩下部分的面积进行计算即可得解.
解答 解:由题意可知,S1=$\frac{1}{2}$,
S2=$\frac{1}{{2}^{2}}$,
S3=$\frac{1}{{2}^{3}}$,
S4=$\frac{1}{{2}^{4}}$=$\frac{1}{16}$,
…,
S2017=$\frac{1}{{2}^{2017}}$,
剩下部分的面积=S2017=$\frac{1}{{2}^{2017}}$,
所以,S1+S2+S3+…+S2017=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{2017}}$=1-$\frac{1}{{2}^{2017}}$,
故答案为:$\frac{1}{16}$,1-$\frac{1}{{2}^{2017}}$.
点评 本题考查图形的变化,关键在于观察出各部分图形的面积之和等于正方形的面积减去剩下部分的面积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
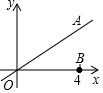 如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.
如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )| A. | a2 | B. | $\frac{3}{2}$a2 | C. | 2a2 | D. | 3a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | |
| B. | 平行于同一条直线的两条直线互相平行 | |
| C. | 同旁内角互补 | |
| D. | 垂直于同一条直线的两条直线互相垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
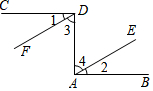 如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
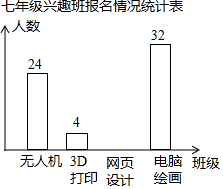 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.| 兴趣班名称 | 频率 |
| “无人机” | a |
| “3D打印” | b |
| “网页设计” | 0.25 |
| “电脑绘画” | 0.4 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com