
ЁОЬтФПЁПФГаЃЮЊСЫНтОХФъМЖФаЩњ1000УзГЄХмЕФГЩМЈЃЌДгжаЫцЛњГщШЁСЫ50УћФаЩњНјааВтЪдЃЌИљОнВтЪдЦРЗжБъзМЃЌНЋЫћУЧЕФЕУЗжНјааЭГМЦКѓЗжЮЊAЁЂBЁЂCЁЂDЫФЕШЃЌВЂЛцжЦГЩЯТУцЕФЦЕЪ§ЗжВМБэКЭЩШаЮЭГМЦЭМ
ЕШМЖ | ГЩМЈЃЈЕУЗжЃЉ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
A | 9ЁЋ10Зж | x | m |
B | 8ЁЋ7 | 23 | 0.46 |
C | 6ЁЋ5 | y | n |
D | 5ЗжвдЯТ | 3 | 0.06 |
ЃЈ1ЃЉЪджБНгаДГіxЃЌyЃЌmЃЌnЕФжЕЃЛ
ЃЈ2ЃЉЧѓБэЪОЕУЗжЮЊCЕШЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЙћИУаЃОХФъМЖЙВгаФаЩњ400УћЃЌЪдЙРМЦет400УћФаЩњжаГЩМЈДяЕНAЕШКЭBЕШЕФШЫЪ§ЙВгаЖрЩйШЫЃП

ЁОД№АИЁПЃЈ1ЃЉЃЉx=19ЃЌy=5ЃЌm=0.38ЃЌn=0.1ЃЈ2ЃЉ36ЁуЃЈ3ЃЉ336
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГібљБОШнСПКЭmЕФжЕЃЌдйНјвЛВНМЦЫуПЩЕУЃЛ
ЃЈ2ЃЉгУ360ЁуГЫвдCЖдгІЕФЦЕТЪМДПЩЕУЃЛ
ЃЈ3ЃЉгУзмШЫЪ§ГЫвдAЁЂBЕФЦЕТЪКЭМДПЩЕУЃЎ
НтЃКЃЈ1ЃЉЁпбљБОШнСПЮЊ23ЁТ0.46ЃН50ЃЌmЃН38%ЃН0.38ЃЌ
ЁрxЃН50ЁС0.38ЃН19ЃЌyЃН50Љ19Љ23Љ3ЃН5ЃЌ
дђnЃН5ЁТ50ЃН0.1ЃЛ
ЃЈ2ЃЉБэЪОЕУЗжЮЊCЕШЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ360ЁуЁС0.1ЃН36ЁуЃЛ
ЃЈ3ЃЉЙРМЦет400УћФаЩњжаГЩМЈДяЕНAЕШКЭBЕШЕФШЫЪ§ЙВга400ЁСЃЈ0.38+0.46ЃЉЃН336ЃЈШЫЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКЕуPЪЧЁїABCФкВПЛђБпЩЯЕФЕуЃЈЖЅЕуГ§ЭтЃЉЃЌдкЁїPABЃЌЁїPBCЃЌЁїPCAжаЃЌШєжСЩйгавЛИіШ§НЧаЮгыЁїABCЯрЫЦЃЌдђГЦЕуPЪЧЁїABCЕФздЯрЫЦЕуЃЎ
Р§ШчЃКШчЭМ1ЃЌЕуPдкЁїABCЕФФкВПЃЌЁЯPBC=ЁЯAЃЌЁЯPCB=ЁЯABCЃЌдђЁїBCPЁзЁїABCЃЌЙЪЕуPЮЊЁїABCЕФздЯрЫЦЕуЃЎ
ЧыФудЫгУЫљбЇжЊЪЖЃЌНсКЯЩЯЪіВФСЯЃЌНтОіЯТСаЮЪЬтЃК
дкЦНУцжБНЧзјБъЯЕжаЃЌЕуMЪЧЧњЯпCЃК![]()
![]() ЩЯЕФШЮвтвЛЕуЃЌЕуNЪЧxжсе§АыжсЩЯЕФШЮвтвЛЕуЃЎ
ЩЯЕФШЮвтвЛЕуЃЌЕуNЪЧxжсе§АыжсЩЯЕФШЮвтвЛЕуЃЎ
ЃЈ1ЃЉ ШчЭМ2ЃЌЕуPЪЧOMЩЯвЛЕуЃЌЁЯONP=ЁЯM, ЪдЫЕУїЕуPЪЧЁїMONЕФздЯрЫЦЕуЃЛ ЕБЕуMЕФзјБъЪЧ![]() ЃЌЕуNЕФзјБъЪЧ
ЃЌЕуNЕФзјБъЪЧ![]() ЪБЃЌЧѓЕуP ЕФзјБъЃЛ
ЪБЃЌЧѓЕуP ЕФзјБъЃЛ
ЃЈ2ЃЉ ШчЭМ3ЃЌЕБЕуMЕФзјБъЪЧ![]() ЃЌЕуNЕФзјБъЪЧ
ЃЌЕуNЕФзјБъЪЧ![]() ЪБЃЌЧѓЁїMONЕФздЯрЫЦЕуЕФзјБъЃЛ
ЪБЃЌЧѓЁїMONЕФздЯрЫЦЕуЕФзјБъЃЛ
ЃЈ3ЃЉ ЪЧЗёДцдкЕуMКЭЕуN,ЪЙЁїMONЮоздЯрЫЦЕу,ЃПШєДцдкЃЌЧыжБНгаДГіетСНЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ



ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁгУ36000дЊЙКНјМзЁЂввСНжжЩЬЦЗЃЌЯњЪлЭъКѓЙВЛёРћ6000дЊЃЎЦфжаМзжжЩЬЦЗУПМўНјМл120дЊЃЌЪлМл138дЊЃЛввжжЩЬЦЗУПМўНјМл100дЊЃЌЪлМл120дЊЃЎ
ЃЈ1ЃЉИУЩЬГЁЙКНјМзЁЂввСНжжЩЬЦЗИїЖрЩйМўЃП
ЃЈ2ЃЉЩЬГЁЕкЖўДЮвддНјМлЙКНјМзЁЂввСНжжЩЬЦЗЃЌЙКНјввжжЩЬЦЗЕФМўЪ§ВЛБфЃЌЖјЙКНјМзжжЩЬЦЗЕФМўЪ§ЪЧЕквЛДЮЕФ2БЖЃЌМзжжЩЬЦЗАДдЪлМлГіЪлЃЌЖјввжжЩЬЦЗДђелЯњЪлЃЎШєСНжжЩЬЦЗЯњЪлЭъБЯЃЌвЊЪЙЕкЖўДЮОгЊЛюЖЏЛёРћВЛЩйгк8160дЊЃЌввжжЩЬЦЗзюЕЭЪлМлЮЊУПМўЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФЗНГЬ(2-a)x2+5x-3=0гаЪЕЪ§Нт,дђећЪ§aЕФзюДѓжЕЪЧ(ЁЁЁЁ)
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃзМБИЙКТђШєИЩЬЈ![]() аЭЕчФдКЭ
аЭЕчФдКЭ![]() аЭДђгЁЛњ.ШчЙћЙКТђ1ЬЈ
аЭДђгЁЛњ.ШчЙћЙКТђ1ЬЈ![]() аЭЕчФдЃЌ2ЬЈ
аЭЕчФдЃЌ2ЬЈ![]() аЭДђгЁЛњЃЌвЛЙВашвЊЛЈЗб6200дЊЃЛШчЙћЙКТђ2ЬЈ
аЭДђгЁЛњЃЌвЛЙВашвЊЛЈЗб6200дЊЃЛШчЙћЙКТђ2ЬЈ![]() аЭЕчФдЃЌ1ЬЈ
аЭЕчФдЃЌ1ЬЈ![]() аЭДђгЁЛњЃЌвЛЙВашвЊЛЈЗб7900дЊЃЎ
аЭДђгЁЛњЃЌвЛЙВашвЊЛЈЗб7900дЊЃЎ
ЃЈ1ЃЉЧѓУПЬЈ![]() аЭЕчФдКЭУПЬЈ
аЭЕчФдКЭУПЬЈ![]() аЭДђгЁЛњЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
аЭДђгЁЛњЕФМлИёЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШчЙћбЇаЃЙКТђ![]() аЭЕчФдКЭ
аЭЕчФдКЭ![]() аЭДђгЁЛњЕФдЄЫуЗбгУВЛГЌЙ§20000дЊЃЌВЂЧвЙКТђ
аЭДђгЁЛњЕФдЄЫуЗбгУВЛГЌЙ§20000дЊЃЌВЂЧвЙКТђ![]() аЭДђгЁЛњЕФЬЈЪ§вЊБШЙКТђ
аЭДђгЁЛњЕФЬЈЪ§вЊБШЙКТђ![]() аЭЕчФдЕФЬЈЪ§Жр1ЬЈЃЌФЧУДИУбЇаЃжСЖрФмЙКТђЖрЩйЬЈ
аЭЕчФдЕФЬЈЪ§Жр1ЬЈЃЌФЧУДИУбЇаЃжСЖрФмЙКТђЖрЩйЬЈ![]() аЭДђгЁЛњЃП
аЭДђгЁЛњЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
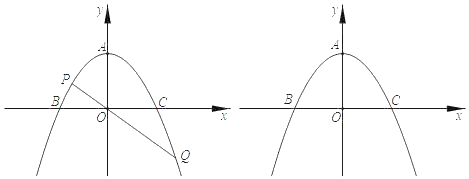
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯп![]() ЕФЖЅЕуЮЊAЃЈ0ЃЌ2ЃЉЃЌгыxжсНЛгкBЃЈЉ2ЃЌ0ЃЉЁЂCЃЈ2ЃЌ0ЃЉСНЕуЃЎ
ЕФЖЅЕуЮЊAЃЈ0ЃЌ2ЃЉЃЌгыxжсНЛгкBЃЈЉ2ЃЌ0ЃЉЁЂCЃЈ2ЃЌ0ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЩшЕуPЪЧХзЮяЯпyЩЯЕФвЛИіЖЏЕуЃЌСЌНгPOВЂбгГЄжСЕуQЃЌЪЙOQЃН2OPЃЎШєЕуQе§КУТфдкИУХзЮяЯпЩЯЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуPЪЧХзЮяЯпyЩЯЕФвЛИіЖЏЕуЃЌСЌНгPOВЂбгГЄжСЕуQЃЌЪЙOQЃНmOPЃЈmЮЊГЃЪ§ЃЉЃЛ
ЂйжЄУїЕуQвЛЖЈТфдкХзЮяЯп![]() ЩЯЃЛ
ЩЯЃЛ
ЂкЩшгавЛИіБпГЄЮЊm+1ЕФе§ЗНаЮЃЈЦфжаmЃО3ЃЉЃЌЫќЕФвЛзщЖдБпДЙжБгкxжсЃЌСэвЛзщЖдБпДЙжБгкyжсЃЌВЂЧвИУе§ЗНаЮЫФИіЖЅЕуе§КУТфдкХзЮяЯп![]() КЭ
КЭ![]() зщГЩЕФЗтБеЭМаЮЩЯЃЌЧѓЯпЖЮPQБЛИУе§ЗНаЮЕФСНЬѕБпНиЕУЯпЖЮГЄзюДѓЪБЕуQЕФзјБъЃЎ
зщГЩЕФЗтБеЭМаЮЩЯЃЌЧѓЯпЖЮPQБЛИУе§ЗНаЮЕФСНЬѕБпНиЕУЯпЖЮГЄзюДѓЪБЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЪЧ_______ЃЎ
ЕФжЕЪЧ_______ЃЎ
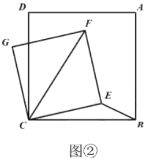
ЃЈ2ЃЉШчЭМЂкЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЦНУцЩЯвЛЖЏЕуЃЌЧв
ЪЧЦНУцЩЯвЛЖЏЕуЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдк
ЃЌдк![]() ЩЯЗНзїе§ЗНаЮ
ЩЯЗНзїе§ЗНаЮ![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
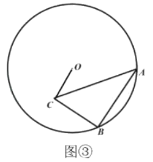
ЮЪЬтНтОіЃКЃЈ3ЃЉШчЭМЂлЃЌ![]() АыОЖЮЊ6ЃЌдк
АыОЖЮЊ6ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дк
дк![]() ФкЃЌЧв
ФкЃЌЧв![]() ЃЎЕБЕу
ЃЎЕБЕу![]() дкдВЩЯдЫЖЏЪБЃЌЧѓЯпЖЮ
дкдВЩЯдЫЖЏЪБЃЌЧѓЯпЖЮ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
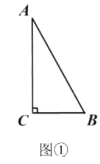
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌABЮЊжБОЖЃЌ ODЁЮBCНЛЁбOгкЕуDЃЌНЛACгкЕуEЃЌСЌНгADЃЌBDЃЌCDЃЎ
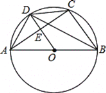
ЃЈ1ЃЉЧѓжЄЃКAD=CDЃЛ
ЃЈ2ЃЉШєAB=10ЃЌcosЁЯABC=![]() ЃЌЧѓtanЁЯDBCЕФжЕЃЎ
ЃЌЧѓtanЁЯDBCЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЃЉгУnИі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁСnОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃПЃЈ2ЁСnОиаЮБэЪООиаЮЕФСкБпЪЧ2КЭnЃЉ
ЃЈЬНОПЃЉВЛЗСМйЩшгаanжжВЛЭЌЕФЯтЧЖЗНАИЃЎЮЊЬНОПanЕФБфЛЏЙцТЩЃЌЮвУЧВЩШЁвЛАуЮЪЬтЬиЪтЛЏЕФВпТдЃЌЯШДгзюМђЕЅЧщаЮШыЪжЃЌдйж№ДЮЕнНјЃЌзюКѓВТЯыЕУГіНсТлЃЎ
ЬНОПвЛЃКгУ1Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС1ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ШчЭМЃЈ1ЃЉЃЌЯдШЛжЛга1жжЯтЧЖЗНАИЃЎЫљвдЃЌa1ЃН1ЃЎ
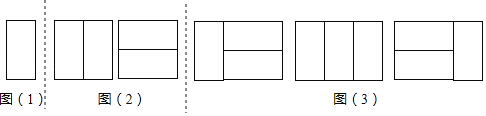
ЬНОПЖўЃКгУ2Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС2ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ШчЭМЃЈ2ЃЉЃЌЯдШЛжЛга2жжЯтЧЖЗНАИЃЎЫљвдЃЌa2ЃН2ЃЎ
ЬНОПШ§ЃКгУ3Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС3ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
вЛРрЃКдкЬНОПвЛУПИіЯтЧЖЭМЕФгвВрдйКсзХЯтЧЖ2Иі2ЁС1ОиаЮЃЌга1жжЯтЧЖЗНАИЃЛ
ЖўРрЃКдкЬНОПЖўУПИіЯтЧЖЭМЕФгвВрдйЪњзХЯтЧЖ1Иі2ЁС1ОиаЮЃЌга2жжЯтЧЖЗНАИЃЛ
ШчЭМЃЈ3ЃЉЃЎЫљвдЃЌa3ЃН1+2ЃН3ЃЎ
ЬНОПЫФЃКгУ4Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС4ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
вЛРрЃКдкЬНОПЖўУПИіЯтЧЖЭМЕФгвВрдйКсзХЯтЧЖ2Иі2ЁС1ОиаЮЃЌгаЁЁ ЁЁжжЯтЧЖЗНАИЃЛ
ЖўРрЃКдкЬНОПШ§УПИіЯтЧЖЭМЕФгвВрдйЪњзХЯтЧЖ1Иі2ЁС1ОиаЮЃЌгаЁЁ ЁЁжжЯтЧЖЗНАИЃЛ
ЫљвдЃЌa4ЃНЁЁ ЁЁЃЎ
ЬНОПЮхЃКгУ5Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС5ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ЃЈЗТееЩЯЪіЗНЗЈЃЌаДГіЬНОПЙ§ГЬЃЌВЛгУЛЭМЃЉ
ЁЁ
ЃЈНсТлЃЉгУnИі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁСnОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ЃЈжБНгаДГіanгыanЉ1ЃЌanЉ2ЕФЙиЯЕЪНЃЌВЛаДНтД№Й§ГЬЃЉЃЎ
ЃЈгІгУЃЉгУ10Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС10ОиаЮЃЌгаЁЁ ЁЁжжВЛЭЌЕФЯтЧЖЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com