
【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
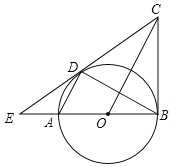
A. 4个B. 3个C. 2个D. 1个
科目:初中数学 来源: 题型:
【题目】已知抛物线G:![]() 有最低点。
有最低点。
(1)求二次函数![]() 的最小值(用含m的式子表示);
的最小值(用含m的式子表示);
(2)将抛物线G向右平移m个单位得到抛物线G1。经过探究发现,随着m的变化,抛物线G1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(3)记(2)所求的函数为H,抛物线G与函数H的图像交于点P,结合图像,求点P的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,将四边形
上,将四边形![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 、
、![]() 的对称点分别记为
的对称点分别记为![]() 、
、![]() .
.
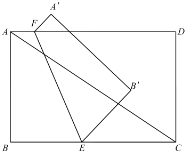
(1)当![]() 时,若点
时,若点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的长;
的长;
(2)设![]() ,若翻折后存在点
,若翻折后存在点![]() 落在线段
落在线段![]() 上,则
上,则![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
(1)当sinB=![]() 时,
时,
①求证:BE=2CD.
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)当sinB=![]() 时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2
时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2![]() ,求线段CD的长.
,求线段CD的长.
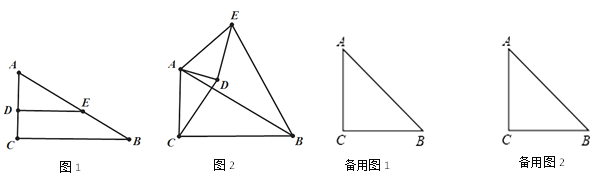
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
(1)证明:四边形AECF是菱形;
(2)求菱形AECF的面积.
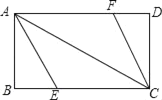
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市要选拔一名教师参加省级评优课比赛:经笔试、面试,结果小潘和小丁并列第一,评委会决定通过摸球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个蓝球,小潘先取出一个球,记住颜色后放回,然后小丁再取出一个球.若两次取出的球都是红球,则小潘胜出;若两次取出的球是一红一蓝,则小丁胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com