
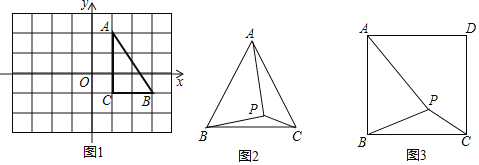
【题目】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B= ;
(2)如图2,在等边三角形ABC内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和等边三角形ABC的边长;
,求∠BPC的度数和等边三角形ABC的边长;
(3)如图3,在正方形ABCD内有一点P,且PA=![]() ,PB=2,PC=
,PB=2,PC=![]() ,求∠BPC的度数和正方形ABCD的边长.
,求∠BPC的度数和正方形ABCD的边长.
【答案】(1)见解析,45°;(2)∠BPC=150°,等边三角形ABC的边长为![]() ;(3)∠BPC=135°,正方形ABCD的边长为
;(3)∠BPC=135°,正方形ABCD的边长为![]() .
.
【解析】
(1)根据旋转角,旋转方向画出图形即可,只要证明△ABB′是等腰直角三角形即可;
(2)将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=1,P′M=![]() ,根据勾股定理即可求出答案;
,根据勾股定理即可求出答案;
(3)将△BPC绕点B逆时针旋转90°得到△AEB,与(1)类似:可得:∠EBP=∠EBA+∠ABP=∠ABC=90°,求出∠BEP=![]() (180°90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°
(180°90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°
解:(1)如图1所示,
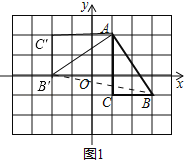
连接BB′,将△ABC绕点A按顺时针方向旋转90°,
∴AB=AB′,∠B′AB=90°,
∴∠AB′B=45°,
故答案为:45°;
(2)∵△ABC是等边三角形,
∴∠ABC=60°,
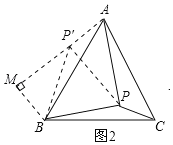
将△BPC绕点B顺时针旋转60°得出△ABP′,如图2,
∴AP′=CP=![]() ,BP′=BP=2,∠PBC=∠P′BA,∠AP′B=∠BPC,
,BP′=BP=2,∠PBC=∠P′BA,∠AP′B=∠BPC,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴PP′=2,∠BP′P=60°,
∵AP′=![]() ,AP=
,AP=![]() ,
,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,则△PP′A是 直角三角形;
∴∠BPC=∠AP′B=90°+60°=150°;
过点B作BM⊥AP′,交AP′的延长线于点M,
∴∠MP′B=30°,BM=1,
由勾股定理得:P′M=![]() ,
,
∴AM=![]() ,
,
由勾股定理得:AB=![]() .
.
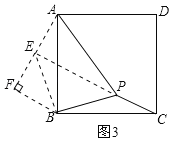
(3)如图3,将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=![]() ,BE=BP=2,∠BPC=∠AEB,∠ABE=∠PBC,
,BE=BP=2,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴∠BEP=![]() (180°﹣90°)=45°,
(180°﹣90°)=45°,
由勾股定理得:EP=![]() ,
,
∵AE=![]() ,AP=
,AP=![]() ,EP=
,EP=![]() ,
,
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°.
∴AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法中,①任意有理数![]() 的倒数是
的倒数是![]() ,②相反数等于自身的数只有一个,③海拔-155米表示海平面下155米,④绝对值大于本身的数一定是负数,⑤零是最小的自然数,⑥有理数包含正有理数和负有理数,⑦任意有理数
,②相反数等于自身的数只有一个,③海拔-155米表示海平面下155米,④绝对值大于本身的数一定是负数,⑤零是最小的自然数,⑥有理数包含正有理数和负有理数,⑦任意有理数![]() 的相反数是
的相反数是![]() .正确的有( )个
.正确的有( )个
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
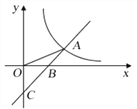
【题目】如图,直线![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点B,与反比例函数
轴交于点B,与反比例函数![]() 的图象在第一象限交于点A,连接OA,且
的图象在第一象限交于点A,连接OA,且![]() .
.
(1)求ΔBOC的面积.
(2)求点A的坐标和反比例函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表)。
月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |

设一个月内使用移动电话主叫的时间为![]() 分(
分(![]() 为正整数),请根据表中提供的信息回答下列问题:
为正整数),请根据表中提供的信息回答下列问题:
(1)用含有![]() 的式子填写下表:
的式子填写下表:
| 150< |
|
| |
方式一计费/元 | 58 |
| 108 |
|
方式二计费/元 | 88 | 88 | 88 |
|
(Ⅰ)当![]() 为何值时,两种计费方式的费用相等?
为何值时,两种计费方式的费用相等?
(Ⅱ)请根据(Ⅰ)和(Ⅱ)的计算及生活经验,直接写出不同时间段,选用哪种计费方式省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
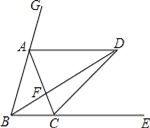
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
求证:①AB=AD;
②CD平分∠ACE.
【答案】详见解析.
【解析】(1)∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
(2)∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
点睛:角平分线问题的辅助线添加及其解题模型.
①垂两边:如图(1),已知![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() ,
, ![]() ,则
,则![]() .
.
②截两边:如图(2),已知![]() 平分
平分![]() ,点
,点![]()
![]() 上,在
上,在![]() 上截取
上截取![]() ,则
,则![]() ≌
≌![]() .
.
③角平分线+平行线→等腰三角形:
如图(3),已知![]() 平分
平分![]() ,
, ![]() ,则
,则![]() ;
;
如图(4),已知![]() 平分
平分![]()
![]() ,则
,则![]() .
.
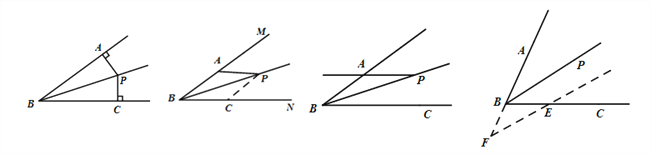
(1) (2) (3) (4)
④三线合一(利用角平分线+垂线→等腰三角形):
如图(5),已知![]() 平分
平分![]() ,且
,且![]() ,则
,则![]() ,
, ![]() .
.
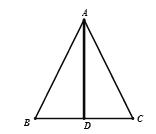
(5)
【题型】解答题
【结束】
26
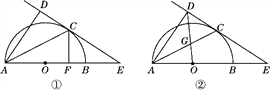
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数y=2x的图象与反比例函数y=![]() 的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )
的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )

A.(﹣8,0)B.(﹣6,0)C.(﹣![]() ,0)D.(﹣
,0)D.(﹣![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数3.3 ,-2 ,0 ,![]() ,-3.5 ;
,-3.5 ;
(1) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(2) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=kx+b(k,b为常数)分别与x轴、y轴交于点A(﹣4,0),B(0,3),抛物线y=﹣x2+4x+1与y轴交于点C,点E在抛物线y=﹣x2+4x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )

A.2B.4C.2.5D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com