
 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).若△CEF与△ABC相似.
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).若△CEF与△ABC相似.分析 若△CEF与△ABC相似.
(1)当AC=BC=2时,△ABC为等腰直角三角形;
(2)当AC=3,BC=4时,分两种情况:
a.若CE:CF=3:4,如答图2所示,此时EF∥AB,CD为AB边上的高;
b.若CF:CE=3:4,如答图3所示.由相似三角形角之间的关系,可以推出∠A=∠ECD与∠B=∠FCD,从而得到CD=AD=BD,即D点为AB的中点.
解答 解:(1)若△CEF与△ABC相似.
当AC=BC=2时,△ABC为等腰直角三角形,如答图1所示.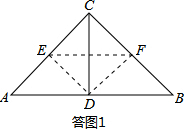
此时D为AB边中点,AD=$\frac{\sqrt{2}}{2}$AC=$\sqrt{2}$;
(2)当AC=3,BC=4时,有两种情况:
a.若CE:CF=3:4,如答图2所示.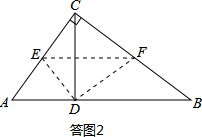
∵CE:CF=AC:BC,
∴EF∥AB,
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高.
在Rt△ABC中,AC=3,BC=4,
∴AB=5,
∴cosA=$\frac{3}{5}$.
AD=AC•cosA=3×$\frac{3}{5}$=1.8;
b.若CF:CE=3:4,如答图3所示.
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴此时AD=$\frac{1}{2}$AB=$\frac{1}{2}$×5=2.5.
综上所述,当AC=3,BC=4时,AD的长为1.8或2.5.
点评 本题考查了几何图形折叠问题和相似三角形的判定与性质.第(2)问需要分两种情况分别计算,此处容易漏解,需要引起注意.


科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -5 | -2 | +4 | +8 | -7 | -12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
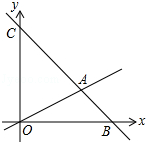 如图,在平面直角坐标系中,直线AC的表达式为y=-x+6,直线AC与直线OA相交于点A(4,2),有一动点M在线段OA和线段AC上运动.
如图,在平面直角坐标系中,直线AC的表达式为y=-x+6,直线AC与直线OA相交于点A(4,2),有一动点M在线段OA和线段AC上运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com