练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简，再求值： （4a2﹣2a﹣8）﹣（a﹣1），其中a=1．

    a2﹣a﹣，﹣. 【解析】试题分析：先化简然后将a的值代入即可求出答案． 试题解析：原式=a2﹣a﹣2﹣a+=a2﹣a﹣ 当a=1时，原式=1﹣1﹣=﹣
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级下册 期中测试卷 题型：解答题

    如图，已知梯形ABCD，AB∥DC，△AOB的面积等于9，△AOD的面积等于6，AB＝7，求CD的长．

    【解析】试题分析： 由题意易得△COD∽△AOB，由此可得： ；由△AOB的面积等于9，△AOD的面积等于6，可得： ，再结合AB=7即可求得CD的长. 试题解析： ∵AB∥DC， ∴△COD∽△AOB， ∴， ∵△AOB的面积等于9，△AOD的面积等于6， ∴， ∴， 又∵AB＝7， ∴， ∴CD＝.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第4章 几何图形初步 单元测试卷 题型：解答题

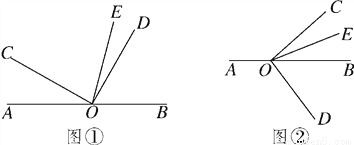
    （12分）已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC.

    （1）如图①，若∠AOC＝30°，求∠DOE的度数；

    （2）在图①中，若∠AOC＝a，直接写出∠DOE的度数（用含a的代数式表示）；

    （3）将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.

    ①探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；

    ②在∠AOC的内部有一条射线OF，且∠AOC－4∠AOF＝2∠BOE＋∠AOF，试确定∠AOF与∠DOE的度数之间的关系，说明理由.

    （1）15°；（2）；（3）①∠AOC＝2∠DOE；②4∠DOE－5∠AOF＝180°. 【解析】试题分析：(1)由已知可求出∠BOC=180°-∠AOC=150°，再由∠COD是直角，OE平分∠BOC求出∠DOE的度数； (2)由(1)可得出结论∠DOE=∠AOC，从而用含a的代数式表示出∠DOE的度数； (3)①由∠COD是直角，OE平分∠BOC可得出∠COE=∠BOE=90...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第4章 几何图形初步 单元测试卷 题型：单选题

    下列说法正确的是（　　）

    A. 两点确定一条直线 B. 两条射线组成的图形叫作角

    C. 两点之间直线最短 D. 若AB＝BC，则点B为AC的中点

    A 【解析】A、两点确定一条直线正确,故本选项正确; B、应为有公共端点的两条射线组成的图形叫做角,故本选项错误; C、应为两点之间线段最短,故本选项错误; D、若AB=BC,则点B为AC的中点错误,因为A、B、C三点不一定共线,故本选项错误. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年山东省德州市六校七年级（上）第一次联考数学试卷 题型：解答题

    先阅读下面文字，然后按要求解题．

    例：1+2+3+…+100=？如果一个一个顺次相加显然太麻烦，我们仔细分析这100个连续自然数的规律和特点，可以发现运用加法的运算律，是可以大大简化计算，提高计算速度的．因为1+100=2+99=3+98=…=50+51=101，所以将所给算式中各加数经过交换、结合以后，可以很快求出结果：

    　1+2+3+4+5+…+100

    =（1+100）+（2+99）+（3+98）+…+（50+51）

    =101× = ．

    （1）补全例题解题过程；

    （2）请猜想：1+2+3+4+5+6+…+（2n﹣2）+（2n﹣1）+2n= ．

    （3）试计算：a+（a+b）+（a+2b）+（a+3b）+…+（a+99b）．

    （1）50；5050；（2）n（2n+1）；（3）100a+4950b． 【解析】试题分析： （1）由题意可得从1到100共有100个数据，两个一组，则共有50组，由此即可补全例题的解题过程； （2）观察、分析所给式子可知，所给代数式中共包含了个式子，这样参照例题方法解答即可； （3）观察、分析所给式子可知，所给代数式中共包含了100个式子，再参照例题方法解答即可； ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年山东省德州市六校七年级（上）第一次联考数学试卷 题型：填空题

    若a、b互为相反数，c、d互为倒数，p的绝对值等于2，则关于x的方程(a+b)x2+3cd•x－p2=0的解为________．

    x= 【解析】试题分析：利用倒数，相反数，以及绝对值的意义求出a+b，cd，p的值，代入方程计算即可求出解． 试题解析：根据题意得：a+b=0，cd=1，p=2或-2， 当p=2时，方程变形为0+3x-4=0，即x=； 当p=-2时，方程变形为0+3x-4=0，即x=， 则方程的解为．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年山东省德州市六校七年级（上）第一次联考数学试卷 题型：单选题

    已知x＝－3是方程k(x＋4)－2k－x＝5的解，则k的值是(　　)

    A. －2 B. 2 C. 3 D. 5

    A 【解析】试题分析：把x=-3代入k（x+4）-2k-x=5， 得：k×（-3+4）-2k+3=5， 解得：k=-2． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型：单选题

    圆桌上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影，如图，已知桌面的直径1.2米，桌面距离地面1米，若灯泡距离地面3米，则地面上阴影部分的面积为（　　）

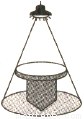
    A. 0.36π平方米 B. 0.81π平方米

    C. 2π平方米 D. 3.24π平方米

    B 【解析】试题解析：如图， 根据常识桌面与地面平行， 所以，△ADE∽△ABC， ∴， 即， 解得BC=1.8， 所以，地面上阴影部分的面积=π•（）2=0.81π平方米． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级年级数学下册第二十九章 达标检测卷 题型：解答题

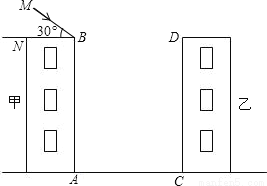
    如图，两幢楼高AB=CD=30m，两楼间的距离AC=24m，当太阳光线与水平线的夹角为30°时，求甲楼投在乙楼上的影子的高度．（结果精确到0.01，≈1.732，≈1.414）

    投到乙楼影子高度是16.14m 【解析】试题分析： （1）首先要作出甲楼投到乙楼的影子，如下图所示,线段CE即表示乙楼的影子； （2）求甲楼投在乙楼上的影子的高度即需求线段CE的长,为此,必须要求出DE的长，而DE为Rt△DEB的边长，且楼间距AC=BD=24m，∠DBE=30°，所以解这个直角三角形即可求解. 【解析】 如图，延长MB交CD于E，连接BD， 由于A...

    查看答案和解析>>

    同步练习册答案