
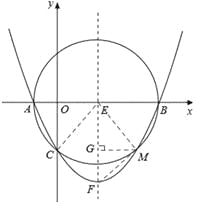
【题目】如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线![]() 经过A,B,C三点,顶点为F.
经过A,B,C三点,顶点为F.

(1)求A,B,C三点的坐标;
(2)求抛物线的解析式及顶点F的坐标;
(3)已知M为抛物线上一动点(不与C点重合),试探究:
①使得以A,B,M为顶点的三角形面积与△ABC的面积相等,求所有符合条件的点M的坐标;
②若探究①中的M点位于第四象限,连接M点与抛物线顶点F,试判断直线MF与⊙E的位置关系,并说明理由.
【答案】(1)A(-2,0),B(8,0),C(0,-4);(2)![]() .F(3,
.F(3,![]() );(3)①点M的坐标为(
);(3)①点M的坐标为(![]() ,4)或(
,4)或(![]() ,4);②直线MF与⊙E相切.理由见解析.
,4);②直线MF与⊙E相切.理由见解析.
【解析】
(1)由题意可直接得到点A、B的坐标,连接CE,在Rt△OCE中,利用勾股定理求出OC的长,则得到点C的坐标.
(2)已知点A、B、C的坐标,利用交点式与待定系数法求出抛物线的解析式,由解析式得到顶点F的坐标.
(3)①△ABC中,底边AB上的高OC=4,若△ABC与△ABM面积相等,则抛物线上的点M须满足条件:|yM|=4.因此解方程yM=4和yM=-4,可求得点M的坐标.
②如解答图,作辅助线,可求得EM=5,因此点M在⊙E上;再利用勾股定理求出MF的长度,则利用勾股定理的逆定理可判定△EMF为直角三角形,∠EMF=90°,所以直线MF与⊙E相切.
解:(1)∵以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,
∴A(-2,0),B(8,0).
如图所,连接CE,
在Rt△OCE中,![]() ,CE=5,
,CE=5,
由勾股定理得:![]() ,
,
∴C(0,-4).
(2)∵点A(-2,0),B(8,0)在抛物线上,
∴设抛物线的解析式为![]() .
.
∵点C(0,-4)在抛物线上,
∴![]() ,解得
,解得![]() .
.
∴抛物线的解析式为:![]() ,即
,即![]() .
.
∵![]() .
.
∴顶点F的坐标为(3,![]() ).
).
(3)①∵△ABC中,底边AB上的高OC=4,
∴若△ABC与△ABM面积相等,则抛物线上的点M须满足条件:|yM|=4.
(I)若yM=4,则![]() ,
,
整理得:![]() ,解得
,解得![]() 或
或![]() .
.
∴点M的坐标为(![]() ,4)或(
,4)或(![]() ,4).
,4).
(II)若yM=-4,则![]() ,
,
整理得:![]() ,解得x=6或x=0(与点C重合,故舍去).
,解得x=6或x=0(与点C重合,故舍去).
∴点M的坐标为(6,-4).
综上所述,满足条件的点M的坐标为:(![]() ,4)或(
,4)或(![]() ,4)或(6,-4).
,4)或(6,-4).
②直线MF与⊙E相切.理由如下:
由题意可知,M(6,-4).
如图,连接EM,MF,过点M作MG⊥对称轴EF于点G,则MG=3,EG=4.
在Rt△MEG中,由勾股定理得:![]() ,
,
∴点M在⊙E上.
由(2)知,F(3,![]() ),∴EF=
),∴EF=![]() .
.
∴![]() .
.
在Rt△MGF中,由勾股定理得: ,
,
在△EFM中,∵![]() ,
,
∴△EFM为直角三角形,∠EMF=90°.
∵点M在⊙E上,且∠EMF=90°,
∴直线MF与⊙E相切.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某种工业原料,甲仓库有12吨,乙仓库有6吨,现需从甲、乙两仓库将这种工业原料分别调往A工厂10吨,B工厂8吨,已知从甲仓库调运1吨原料到A,B两工厂的运费分别是40元和80元,从乙仓库调运1吨原料到A,B两工厂的运费分别是30元和50元.
(1)若总运费为900元,则从甲仓库调运到A工厂的原料为多少吨?
(2)要使总运费最低,应如何安排调运方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若矩形的一个短边与长边的比值为![]() ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
(3)归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正确的是( )
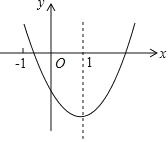
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度.小正方形的顶点称为格点![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() .
.
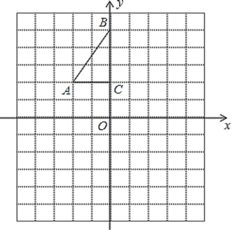
(1)将![]() 以点
以点![]() 为旋转中心旋转
为旋转中心旋转![]() ,得到
,得到![]() ,请画出的图形
,请画出的图形![]() ;
;
(2)平移![]() ,使点
,使点![]() 的对应点
的对应点![]() 坐标为
坐标为![]() ,请画出平移后对应的
,请画出平移后对应的![]() ;
;
(3)若将![]() 绕某一点旋转可得到
绕某一点旋转可得到![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(4)请画出一个以![]() 为对角线,面积是20的菱形
为对角线,面积是20的菱形![]() (要求
(要求![]() ,
,![]() 是格点).
是格点).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个游戏的中奖概率是![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B. 为了解全国中学生的心理健康情况,应该采用普查的方式
C. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
D. 若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
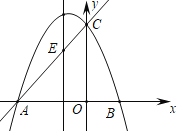
【题目】如图,在平面直角坐标系中,抛物线经过点![]() 、
、![]() 、
、![]() .
.
(1)求抛物线的解析式;
(2)若![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径作圆,
长为半径作圆,![]() 与
与![]() 轴的位置关系如何?请说明理由.
轴的位置关系如何?请说明理由.
(3)过点![]() 作
作![]() 的切线
的切线![]() ,交
,交![]() 轴于点
轴于点![]() ,请求出直线
,请求出直线![]() 的解析式及
的解析式及![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
(1)请用列表或画树状图的方法表示取出数字的所有结果;
(2)求正比例函数y=kx的图象经过第一、三象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com