
分析 (1)进水口工效为$\frac{1}{2}$,出水口为$\frac{1}{5}$,两次补水之间相隔就是出水口放出$\frac{2}{3}$水量时的时间,即:(1-$\frac{1}{3}$)÷$\frac{1}{5}$=$\frac{10}{3}$小时,每次补水时是进出两管一同开放,所以进的速度相当于$\frac{1}{2}$-$\frac{1}{5}$,列式为:(1-$\frac{1}{3}$)$÷(\frac{1}{2}$-$\frac{1}{5})$得出时间;
(2)先计算两次补水的间隔时间就是出水口放出一定的水量还余满水量的m倍时所用的时间,列式为:t1=(1-m)÷$\frac{1}{5}$,再计算每次的补水时间为:t2=(1-m)$÷(\frac{1}{2}-\frac{1}{5})$=$\frac{10}{3}(1-m)$,所以t1≠t2,相比后得$\frac{{t}_{1}}{{t}_{2}}$=$\frac{5(1-m)}{\frac{10}{3}(1-m)}$=$\frac{3}{2}$,则2t1=3t2.
解答 解:(1)当m=$\frac{1}{3}$时,间隔的时间为:(1-$\frac{1}{3}$)÷$\frac{1}{5}$=$\frac{10}{3}$(小时),
每次补水的时间:(1-$\frac{1}{3}$)$÷(\frac{1}{2}$-$\frac{1}{5})$=$\frac{20}{9}$(小时),
答:两次补水之间相隔$\frac{10}{3}$小时,每次补水需要$\frac{20}{9}$小时;
(2)由题意得:m≥$\frac{1}{3}$,
∵(1-m)÷$\frac{1}{5}$≠(1-m)$÷(\frac{1}{2}-\frac{1}{5})$,
∴两次补水的间隔时间和每次的补水时间肯定不相等,
间隔的时间为t1:5(1-m),
每次补水的时间t2:(1-m)$÷(\frac{1}{2}-\frac{1}{5})$=$\frac{10}{3}$(1-m),
∴$\frac{{t}_{1}}{{t}_{2}}$=$\frac{5(1-m)}{\frac{10}{3}(1-m)}$=$\frac{3}{2}$,
∴2t1=3t2.
点评 本题考查了列代数式和求代数式的值,属于工作量问题,本题的总水量看作为1,明确时间=总水量÷工作效率;此题有难度,要注意理解进水口补满后关闭,出水口一直打开.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
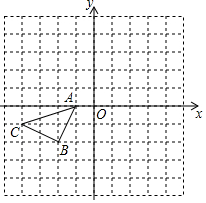 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com