练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求证：相邻补角的平分线互相垂直．

    答案：略
    解析：

    证明：∵OE平分∠AOB，OF平分∠BOC，

    ∴∠1=∠AOB，∠2=∠BOC．

    又∵∠AOB，∠BOC互为邻补角，

    ∴∠AOB＋∠BOC=180°．

    ∴∠1＋∠2=(∠AOB＋∠BOC)=90°．

    ∴OE⊥OF．


    提示：

    原题证明可转化为此题证明．已知如图，∠AOB，∠BOC互为邻补角，OE平分∠AOB，OF平分∠BOC．求证：OE⊥OF．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

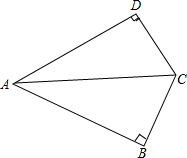    精英家教网已知：如图，四边形ABCD中，AC平分∠BAD，∠B和∠D都是直角．
    （1）求证：BC=CD．
    （2）若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”，其余条件不变，猜想：BC边和邻边CD的长度是否一定相等？请证明你的结论．
    （3）探究：在（2）的情况下，如果再限制∠BAD=60°，那么相邻两边AB、AD和对角线AC之间有什么确定的数量关系？需说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，四边形ABCD中，AC平分∠BAD，∠B和∠D都是直角.

    ⑴ 求证：BC=CD.

    ⑵ 若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变，猜想：BC边和邻边CD的长度是否一定相等？请证明你的结论.

    ⑶ 探究：在⑵的情况下，如果再限制∠BAD=60°，那么相邻两边AB、AD和对角线AC之间有什么确定的数量关系？需说明理由.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，四边形ABCD中，AC平分∠BAD，∠B和∠D都是直角.

    ⑴ 求证：BC=CD.
    ⑵ 若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变，猜想：BC边和邻边CD的长度是否一定相等？请证明你的结论.
    ⑶ 探究：在⑵的情况下，如果再限制∠BAD=60°，那么相邻两边AB、AD和对角线AC之间有什么确定的数量关系？需说明理由.

    查看答案和解析>>

    科目：初中数学 来源：2012届山东宁津县中考二模数学卷（带解析） 题型：解答题

    已知：如图，四边形ABCD中，AC平分∠BAD，∠B和∠D都是直角.

    ⑴ 求证：BC=CD.
    ⑵ 若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变，猜想：BC边和邻边CD的长度是否一定相等？请证明你的结论.
    ⑶ 探究：在⑵的情况下，如果再限制∠BAD=60°，那么相邻两边AB、AD和对角线AC之间有什么确定的数量关系？需说明理由.

    查看答案和解析>>

    同步练习册答案