
【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: 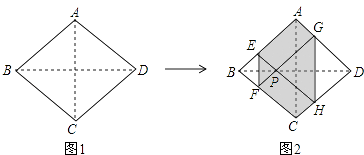
①当x=1时,点P是正方形ABCD的中心;
②当x= ![]() 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的是(写出所有正确判断的序号).
【答案】①④
【解析】解:(1)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,
∴△BEF和△DGH是等腰直角三角形,
∴当AE=1时,重合点P是BD的中点,
∴点P是正方形ABCD的中心;
故①结论正确,(2)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,
∴△BEF∽△BAC,
∵x= ![]() ,
,
∴BE=2﹣ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴EF= ![]() AC,
AC,
同理,GH= ![]() AC,
AC,
∴EF+GH=AC,
故②结论错误,(3)六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积.
∵AE=x,
∴六边形AEFCHG面积=22﹣ ![]() BEBF﹣
BEBF﹣ ![]() GDHD=4﹣
GDHD=4﹣ ![]() ×(2﹣x)(2﹣x)﹣
×(2﹣x)(2﹣x)﹣ ![]() xx=﹣x2+2x+2=﹣(x﹣1)2+3,
xx=﹣x2+2x+2=﹣(x﹣1)2+3,
∴六边形AEFCHG面积的最大值是3,
故③结论错误,(4)当0<x<2时,
∵EF+GH=AC,
六边形AEFCHG周长=AE+EF+FC+CH+HG+AG=(AE+CH)+(FC+AG)+(EF+GH)=2+2+2 ![]() =4+2
=4+2 ![]()
故六边形AEFCHG周长的值不变,
故④结论正确.
所以答案是:①④.
【考点精析】本题主要考查了正方形的性质和翻折变换(折叠问题)的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人分别从A、B两地同时出发.相向而行,甲的速度是每分钟60米,乙的速度是每分钟90米,出发x分钟后,两人恰好相距100米,则A、B两地之间的距离是米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有ADCE中,DE最小的值是( ) 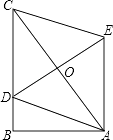
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com