
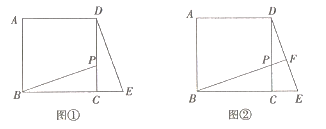
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
【答案】探究:90;应用:![]() ;拓展:42
;拓展:42
【解析】
(1)由旋转性质即可得到旋转角的度数;
(2)由旋转的性质,得到![]() ≌
≌![]() ,由全等三角形对应角相等,得到
,由全等三角形对应角相等,得到![]() ,再由直角三角形两个锐角互余和等量代换,即可得到
,再由直角三角形两个锐角互余和等量代换,即可得到![]() ,即
,即![]() ;
;
(3)由![]() ≌
≌![]() ,得到CE=PC,由DP=2CP,BC=6,得CE=2,则四边形ABED的面积=S正方形ABCD+S△CDE.
,得到CE=PC,由DP=2CP,BC=6,得CE=2,则四边形ABED的面积=S正方形ABCD+S△CDE.
探究:由旋转性质可得旋转角=∠BCD=∠DCE=90°;
故答案为:90°;
应用:由旋转,得![]() ≌
≌![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
拓展:∵![]() ≌
≌![]() ,
,
∴CE=PC,
∵DP=2CP,BC=6,
∴CE=2,
∴S四边形ABED =S正方形ABCD+S△CDE=6×6+![]() ×6×2=36+6=42,
×6×2=36+6=42,
故答案为:42.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0, ![]() ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为
),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为 ![]() .
.
(1)求a的值;
(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;
(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正.减产记为负):
(1) 写出该厂星期一生产工艺品的数量;
(2) 本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3) 请求出该工艺厂在本周实际生产工艺品的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ; (4)
; (4) ![]()
【解析】试题分析:(1)分子、分母分解因式后约分即可;
(2)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可;
(3)第二个分式分子、分母分解因式后约分,然后通分转化为同分母分式,最后依照同分母分式的加减法则计算即可;
(4)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可.
试题解析:
解:(1)原式=
=![]() ;
;
(2)原式=![]()
=![]()
=![]() ;
;
(3)原式=![]()
=![]()
=![]()
=![]()
=![]() ;
;
(4)原式=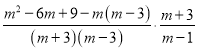
=![]()
=![]() .
.
点睛:此题考查了分式的混合运算,熟练掌握运算法则和运算顺序是解本题的关键.
【题型】解答题
【结束】
20
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3.
<3.
∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2,
﹣2,
∴1<![]() ﹣1<2
﹣1<2
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
解决问题:已知:a是![]() ﹣3的整数部分,b是
﹣3的整数部分,b是![]() ﹣3的小数部分,
﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com