
 如图,?ABCD的边AD=2AB,AE=BF=AB,EC交AD于点M,FD交BC于点N,求证:四边形CDMN是菱形.
如图,?ABCD的边AD=2AB,AE=BF=AB,EC交AD于点M,FD交BC于点N,求证:四边形CDMN是菱形. 分析 △AEM≌△DCM.利用“平行四边形ABCD的对边平行且相等”的性质推知AB∥CD,AB=CD.然后结合已知条件和全等三角形的判定定理AAS证得,由四边形CDMN的对边MD=NC且MD∥NC推知四边形CDMN是平行四边形.再由MD=DC证得平行四边形CDMN是菱形.
解答 证明:在平行四边形ABCD中,AB∥CD,AB=CD.
∵点E、A、B、F在一条直线上,
∴AE∥CD,
∴∠AEM=∠MCD.
又∵AE=AB,
∴AE=DC.
在△AEM与△DCM中,
$\left\{\begin{array}{l}{∠AME=∠DMC}\\{∠AEM=∠DCM}\\{AE=DC}\end{array}\right.$,
∴△AEM≌△DCM(AAS);
在平行四边形ABCD中,AD∥BC,AD=BC,AB=CD.
∵△AEM≌△DCM,则AM=DM,即MD=$\frac{1}{2}$AD,
同理,易证△BFN≌△CDN,则BN=CN,即CN=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴MD=CN,
又MD∥NC,
∴四边形CDMN是平行四边形.
又∵2AB=AD=2DM,AB=CD,
∴DM=CD,
∴平行四边形CDMN是菱形.
点评 本题考查了全等三角形的判定与性质、平行四边形的判定与性质以及菱形的判定.注意:菱形的邻边相等的平行四边形,而不是邻边相等的四边形.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,某村有一个四边形池塘,它的四个顶点A,B,C,D处均有一棵大树、村里准备开挖池塘建鱼塘.想使池塘的面积扩大一倍,又想保持大树在池塘边不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一设想?若能,请你设计出所要求的平行四边形;若不能,请说明理由.
如图,某村有一个四边形池塘,它的四个顶点A,B,C,D处均有一棵大树、村里准备开挖池塘建鱼塘.想使池塘的面积扩大一倍,又想保持大树在池塘边不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一设想?若能,请你设计出所要求的平行四边形;若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-y={(\sqrt{-y})^2}(y<0)$ | B. | $-7={(\root{3}{-7})^3}$ | C. | $-7={(\sqrt{-7})^2}$ | D. | $-11=-\sqrt{(-11}{)^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A,B,C,D 四点在同一条直线上,AB=CD,AE=BF,CE=DF.则下列结论正确的是( )
如图,A,B,C,D 四点在同一条直线上,AB=CD,AE=BF,CE=DF.则下列结论正确的是( )| A. | △ACE和△BDF成轴对称 | B. | △ACE经过旋转可以和△BDF重合 | ||
| C. | △ACE和△BDF成中心对称 | D. | △ACE经过平移可以和△BDF重合 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
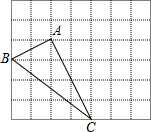 如图,每个小正方形的边长均为1个长度单位的网格中,有一个△ABC,三角形的三个顶点均在网格的顶点上.
如图,每个小正方形的边长均为1个长度单位的网格中,有一个△ABC,三角形的三个顶点均在网格的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC∥BD,AD与BC交于点E,过点E作EF∥BD,交线段AB于点F,则下列各式错误的是( )
如图,AC∥BD,AD与BC交于点E,过点E作EF∥BD,交线段AB于点F,则下列各式错误的是( )| A. | $\frac{AF}{BF}$=$\frac{AE}{DE}$ | B. | $\frac{BF}{AF}$=$\frac{BE}{CE}$ | C. | $\frac{AE}{AD}$+$\frac{BE}{BC}$=1 | D. | $\frac{AF}{BF}$=$\frac{CE}{DE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,对角线AC,BD交于点O,OE平分∠ACD,分别交AD,BD于E,EF∥AC交CD于F,连接OE.下列结论:
如图,在正方形ABCD中,对角线AC,BD交于点O,OE平分∠ACD,分别交AD,BD于E,EF∥AC交CD于F,连接OE.下列结论:| A. | ②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com