



 .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
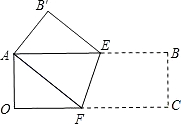
 23、观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.
23、观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分) 1.(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′ 处(如图1),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.(3分)

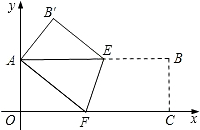
2.(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.(4+3分)

查看答案和解析>>
科目:初中数学 来源: 题型:
观察与发现:将矩形纸片A![]() OCB折叠,使点C与点A重合,点B落在点B′ 处 (如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.
OCB折叠,使点C与点A重合,点B落在点B′ 处 (如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2015届江苏昆山兵希中学初二上第二次阶段测试数学卷(解析版) 题型:解答题
(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.

(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com