
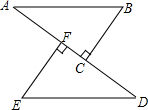
 如图,AB=DE,BC⊥AD,EF⊥AD,垂足分别为C、F,且AF=DC,求证:AB∥DE.
如图,AB=DE,BC⊥AD,EF⊥AD,垂足分别为C、F,且AF=DC,求证:AB∥DE. 科目:初中数学 来源: 题型:解答题
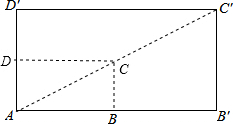 如图,矩形ABCD与矩形AB′C′D′是位似图形,已知矩形ABCD的周长是25cm,BB′=4cm,DD′=2cm,求矩形ABCD和AB′C′D′的面积比.
如图,矩形ABCD与矩形AB′C′D′是位似图形,已知矩形ABCD的周长是25cm,BB′=4cm,DD′=2cm,求矩形ABCD和AB′C′D′的面积比.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
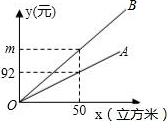 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com